题目内容
设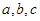 是互不相等的正数,
是互不相等的正数,
求证:(Ⅰ)
(Ⅱ)
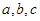 是互不相等的正数,
是互不相等的正数,求证:(Ⅰ)

(Ⅱ)

见解析。
本试题主要是考查了重要不等式和均值不等式的运用证明不等式的问题。
(1)直接运用综合法思想得到不等式的证明
(2)因为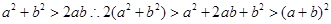 ,然后
,然后 两边开方得到结论,相加。
两边开方得到结论,相加。
(I)∵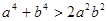 ,
,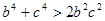 ,
,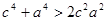
∴
∵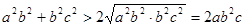
同理: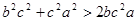 ,
,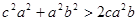 ,
,
∴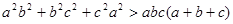 ……………6分
……………6分
(II)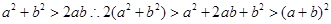
即 ,两边开平方得
,两边开平方得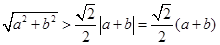
同理可得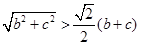
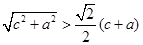 三式相加,得
三式相加,得
 …………..12分
…………..12分
(1)直接运用综合法思想得到不等式的证明
(2)因为
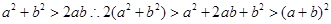 ,然后
,然后 两边开方得到结论,相加。
两边开方得到结论,相加。(I)∵
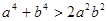 ,
,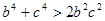 ,
,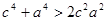
∴

∵
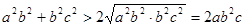
同理:
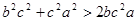 ,
,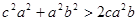 ,
,∴
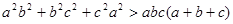 ……………6分
……………6分(II)
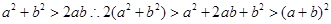
即
 ,两边开平方得
,两边开平方得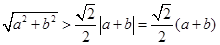
同理可得
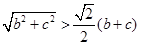
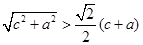 三式相加,得
三式相加,得 …………..12分
…………..12分
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
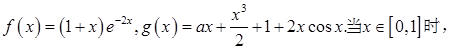

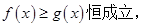
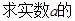 取值范围.
取值范围. -1,证明:
-1,证明: (x-1);
(x-1); .
. , 求证:
, 求证: .
.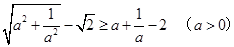
 ,
, .若
.若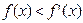 对定义域内的
对定义域内的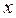 恒成立,则称函数
恒成立,则称函数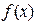 为
为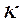 函数.(1)请举出一个定义域为
函数.(1)请举出一个定义域为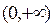 的
的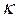 函数,并说明理由;(2)对于定义域为
函数,并说明理由;(2)对于定义域为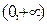 的
的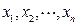 ,均有
,均有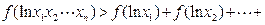
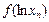 ;
;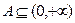 的
的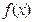 ,求证:
,求证: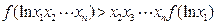 .
. ,1+
,1+ >1,1+
>1,1+ +
+ + +
+ + >
> ,1+
,1+ >2,1+
>2,1+ >
> , ,由此猜测第n个不等式为 (n∈N*).
, ,由此猜测第n个不等式为 (n∈N*).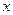 是正实数,求证:
是正实数,求证: ;
;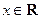 ,不等式
,不等式