题目内容
某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
| 1 |
| 3 |
| 10000 |
| x |
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
分析:(1)分两种情况进行研究,当0<x<80时,投入成本为C(x)=
x2+10x(万元),根据年利润=销售收入-成本,列出函数关系式,当x≥80时,投入成本为C(x)=51x+
-1450,根据年利润=销售收入-成本,列出函数关系式,最后写成分段函数的形式,从而得到答案;
(2)根据年利润的解析式,分段研究函数的最值,当0<x<80时,利用二次函数求最值,当x≥80时,利用基本不等式求最值,最后比较两个最值,即可得到答案.
| 1 |
| 3 |
| 10000 |
| x |
(2)根据年利润的解析式,分段研究函数的最值,当0<x<80时,利用二次函数求最值,当x≥80时,利用基本不等式求最值,最后比较两个最值,即可得到答案.
解答:解:(1)∵每件商品售价为0.05万元,
∴x千件商品销售额为0.05×1000x万元,
①当0<x<80时,根据年利润=销售收入-成本,
∴L(x)=(0.05×1000x)-
x2-10x-250=-
x2+40x-250;
②当x≥80时,根据年利润=销售收入-成本,
∴L(x)=(0.05×1000x)-51x-
+1450-250=1200-(x+
).
综合①②可得,L(x)=
.
(2)由(1)可知,L(x)=
,
①当0<x<80时,L(x)=-
x2+40x-250=-
(x-60)2+950,
∴当x=60时,L(x)取得最大值L(60)=950万元;
②当x≥80时,L(x)=1200-(x+
)≤1200-2
=1200-200=1000,
当且仅当x=
,即x=100时,L(x)取得最大值L(100)=1000万元.
综合①②,由于950<1000,
∴当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.
∴x千件商品销售额为0.05×1000x万元,
①当0<x<80时,根据年利润=销售收入-成本,
∴L(x)=(0.05×1000x)-
| 1 |
| 3 |
| 1 |
| 3 |
②当x≥80时,根据年利润=销售收入-成本,
∴L(x)=(0.05×1000x)-51x-
| 10000 |
| x |
| 10000 |
| x |
综合①②可得,L(x)=
|
(2)由(1)可知,L(x)=
|
①当0<x<80时,L(x)=-
| 1 |
| 3 |
| 1 |
| 3 |
∴当x=60时,L(x)取得最大值L(60)=950万元;
②当x≥80时,L(x)=1200-(x+
| 10000 |
| x |
x•
|
当且仅当x=
| 10000 |
| x |
综合①②,由于950<1000,
∴当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.
点评:本小题主要考查函数模型的选择与应用.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.本题建立的数学模型为分段函数,对于分段函数的问题,一般选用分类讨论和数形结合的思想方法进行求解.属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
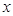 千件,需另投入成本为
千件,需另投入成本为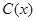 (万元),当年产量不足80千件时,
(万元),当年产量不足80千件时,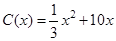 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,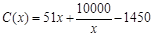 (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.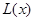 (万元)关于年产量
(万元)关于年产量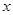 千件,需另投入成本为
千件,需另投入成本为 ,当年产量不足80千件时,
,当年产量不足80千件时,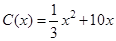 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.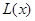 (万元)关于年产量
(万元)关于年产量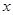 千件,需另投入成本为
千件,需另投入成本为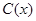 ,当年产量不足80千件时,
,当年产量不足80千件时,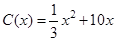 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,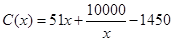 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.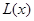 (万元)关于年产量
(万元)关于年产量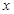 千件,需另投入成本为
千件,需另投入成本为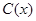 ,当年产量不足80千件时,
,当年产量不足80千件时,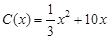 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,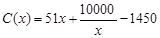 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.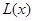 (万元)关于年产量
(万元)关于年产量