题目内容
如图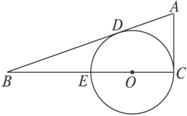
图
解析:∵CO∶OB=1∶3,OC=OE,
∴BE∶EC=1∶1.
设BE=x,则BC=2x.
由切割线定理得BD2=BE·BC=2x2,
∴BD=
.
又由切线长定理得AD=AC,
在Rt△ABC中,AB2=AC2+BC2,
∴(
+2)2=22+(2x)2.
解得x=
.
答案: 
练习册系列答案
相关题目
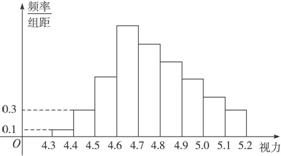
现有A、B两个班级,每个班级各有45名学生参加一次测验,每名参加者可获得0,1,2,3,4,5,6,7,8,9分这几种不同分值中的一种,A班的测试结果如下表所示：
分数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数 | 1 | 3 | 5 | 7 | 6 | 8 | 6 | 4 | 3 | 2 |
B班的成绩如图2-2-16所示.
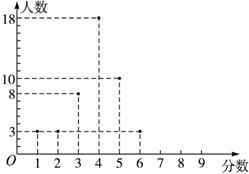
图2-2-16
(1)你认为哪个班级的成绩比较稳定？
(2)若两班共有60人及格,则参加者最少获得多少分才可能及格？
