题目内容
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知在全部105人中随机抽取1人为优秀的概率为
(Ⅰ)请完成上面的列联表;
(Ⅱ)把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和作为被抽取人的序号,试求抽到序号为6号或10号学生的概率.
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 105 |
| 2 |
| 7 |
(Ⅰ)请完成上面的列联表;
(Ⅱ)把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和作为被抽取人的序号,试求抽到序号为6号或10号学生的概率.
分析:(1)由全部105人中抽到随机抽取1人为优秀的概率为
,我们可以计算出优秀人数为30,我们易得到表中各项数据的值.
(2)找出满足条件抽到6或10号的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.
| 2 |
| 7 |
(2)找出满足条件抽到6或10号的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.
解答:解:(1)∵全部105人中抽到随机抽取1人为优秀的概率为
,
∴我们可以计算出优秀人数为
×105=30,得乙班优秀人数30-10=20,列联表为:
(2)设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y).
所有的基本事件有(1,1)、(1,2)、(1,3)、(6,6),共36个.
事件A包含的基本事件有:(1,5)、(2,4)、(3,3)、(4,2)、
(5,1)(4,6)、(5,5)、(6、4),共8个
∴P(A)=
=
| 2 |
| 7 |
∴我们可以计算出优秀人数为
| 2 |
| 7 |
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
所有的基本事件有(1,1)、(1,2)、(1,3)、(6,6),共36个.
事件A包含的基本事件有:(1,5)、(2,4)、(3,3)、(4,2)、
(5,1)(4,6)、(5,5)、(6、4),共8个
∴P(A)=
| 8 |
| 36 |
| 2 |
| 9 |
点评:本题考查列联表,考查古典概型概率的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从甲、乙两个班级各随机抽取10名同学的数学成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
(I)试完成甲班制取10名同学数学成绩频率分布表,并估计甲班的及格率.
(II)从每班抽取的同学中各抽取一人,求至少有一人及格的概率.

(I)试完成甲班制取10名同学数学成绩频率分布表,并估计甲班的及格率.
| 分组 | 频数 | 频率 |
| [70,80) | ||
| [80,90) | ||
| [90,100) | ||
| [100,110) |

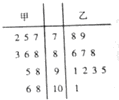 从甲、乙两个班级各随机抽取10名同学的数学成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
从甲、乙两个班级各随机抽取10名同学的数学成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.