题目内容
已知公差不为零的等差数列{an}的前4项和为10,且a2,a3,a7成等比数列.
(Ⅰ)求通项公式an
(Ⅱ)设bn=2an,求数列{bn}的前n项和Sn.
(Ⅰ)求通项公式an
(Ⅱ)设bn=2an,求数列{bn}的前n项和Sn.
(I)由题意可得,
∵d≠0
∴
∴an=3n-5
(II)∵bn=2an=23n-5=
•8n-1
∴数列{an}是以
为首项,以8为公比的等比数列
∴Sn=
=
|
∵d≠0
∴
|
∴an=3n-5
(II)∵bn=2an=23n-5=
| 1 |
| 4 |
∴数列{an}是以
| 1 |
| 4 |
∴Sn=
| ||
| 1-8 |
| 8n-1 |
| 28 |

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
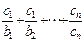 =an+1成立,求
=an+1成立,求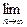
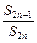

 中,已知
中,已知 则
则 的最大值为 。
的最大值为 。