题目内容
已知抛物线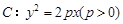 的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设
的焦点为F,准线为l,过F的直线与该抛物线交于A、B两点,设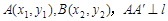 于
于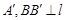 于
于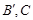 为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②
为弦AB的中点,则下列结论:①以AB为直径的圆必与准线l相切; ②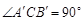 ;
;
③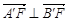 ; ④
; ④ ; ⑤.
; ⑤.
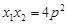
其中一定正确的有 (写出所有正确结论的序号).
【答案】
①③④.
【解析】
试题分析:通过设出直线方程y=k(x-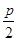 )与抛物线联立方程组得到可知①以AB为直径的圆必与准线l相切;成立,②
)与抛物线联立方程组得到可知①以AB为直径的圆必与准线l相切;成立,②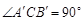 ,不成立。
,不成立。
对于③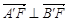 ,利用平行性来证明成立,对于④
,利用平行性来证明成立,对于④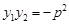 ;根据韦达定理可知成立, 对于⑤.
;根据韦达定理可知成立, 对于⑤.  错误,应该是
错误,应该是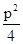 故可知答案为①③④.
故可知答案为①③④.
考点:直线与抛物线
点评:解决的关键是根据直线与抛物线的位置关系以及抛物线定义来求解,属于中档题。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 的焦点为F,过F的直线交抛物线于M、N两点,其准线
的焦点为F,过F的直线交抛物线于M、N两点,其准线 与x轴交于K点.
与x轴交于K点.
 的最小值.
的最小值. 的焦点为F,过抛物线在第一象限部分上一点P的切线为
的焦点为F,过抛物线在第一象限部分上一点P的切线为 ,过P点作平行于
,过P点作平行于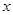 轴的直线
轴的直线 ,过焦点F作平行于
,过焦点F作平行于 ,则点P的坐标为 。
,则点P的坐标为 。 的焦点为F,过点F作直线
的焦点为F,过点F作直线 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与 轴交于点C。
轴交于点C。 ;
; 的最大值,并求
的最大值,并求 的焦点为F,过点
的焦点为F,过点 的直线
的直线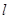 与
与 相交于
相交于 、
、 两点,点A关于
两点,点A关于 轴的对称点为D .
轴的对称点为D . ,求
,求 的内切圆M的方程 .
的内切圆M的方程 . 的焦点为F,准线为
的焦点为F,准线为 ,经过F且斜率为
,经过F且斜率为 的直线与抛物线在
的直线与抛物线在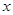 轴上方的部分相交于点A,且AK
轴上方的部分相交于点A,且AK
 的面积是( )
的面积是( ) C
C  D 8
D 8