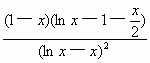题目内容
已知函数f(x)=2x+alnx.
(1)若f(x)在[1,+∞)上为增函数,求a的范围
(2)若a<0,对于任意两个正数x1、x2总有:![]()
(3)若存在x∈[1,e],使不等式f(x)≤(a+3)x-![]() x2成立,求实数a的取值范围
x2成立,求实数a的取值范围
答案:
解析:
解析:
|
(1)当x≥1时, (2)作差变形可得: ∴ln 即 (3) ∴lnx≤1≤x,因等号不能同时取到,∴lnx<x,lnx-x<0 ∴a≥ 令 从而, 由题设a≥- 即存在x |

练习册系列答案
相关题目
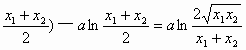 (*)
(*)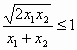
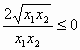 ,又a<0 ∴(*)式≥0
,又a<0 ∴(*)式≥0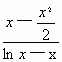
 ,x
,x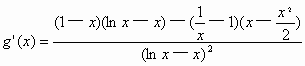 =
=