题目内容
已知椭圆的一个焦点F1(0,-2![]() ),对应的准线方程为y=-
),对应的准线方程为y=-![]() ,且离心率e满足:
,且离心率e满足:![]() ,e,
,e,![]() 成等比数列.
成等比数列.
(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线x=-![]()
平分.若存在,求出l的倾斜角的范围;若不存在,请说明理由.
(1)x2+![]() y2=1;(2)存在,直线l倾斜角α∈(
y2=1;(2)存在,直线l倾斜角α∈(![]() ,
,![]() )∪(
)∪(![]() ,
,![]() )。
)。
解析:
依题意e=![]() .
.
(1)∵![]() -c=
-c=![]()
∴a=3,c=2![]() ,b=1,
,b=1,
又F1(0,-2![]() ),对应的准线方程为y=-
),对应的准线方程为y=-![]() .
.
∴椭圆中心在原点,所求方程为x2+![]() y2=1
y2=1
(2)假设存在直线l,依题意l交椭圆所得弦MN被x=-![]() 平分,∴直线l的斜率
平分,∴直线l的斜率
存在.设直线l:y=kx+m
由 消去y,整理得
消去y,整理得
(k2+9)x2+2kmx+m2-9=0
∵l与椭圆交于不同的两点M,N,
∴Δ=4k2m2-4(k2+9)(m2-9)>0
即m2-k2-9<0 ①
设M(x1,y1),N(x2,y2)
∴![]() ,
,
∴m=![]() ②
②
把②代入①式中得
![]() -(k2+9)<0
-(k2+9)<0
∴k>![]() 或k<-
或k<-![]()
∴直线l倾斜角α∈(![]() ,
,![]() )∪(
)∪(![]() ,
,![]() )
)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
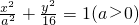 的一个焦点F(3,0),则a=________.
的一个焦点F(3,0),则a=________. 的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为
的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为45°的直线l过点F,
,倾斜角为45°的直线l过点F, 的一个焦点F(3,0),则a= .
的一个焦点F(3,0),则a= . 的一个焦点F(3,0),则a= .
的一个焦点F(3,0),则a= .