题目内容
已知直线l:
(t为参数),曲线C:
(θ为参数),直线l与曲线C交于A、B两点,若点P的坐标为(1,-1),则|PA|•|PB=|______.
|
|
由曲线C:
(θ为参数)化为x2+y2=1.
把直线l:
(t为参数)化为
(*).
把(*)代入曲线C的方程可得:(1-
m)2+(-1+
m)2=1,
化为m2-(1+
)m+1=0,∴m1m2=1.
根据参数的几何意义可得:|PA|•|PB|=m1m2=1.
故答案为:1.
|
把直线l:
|
|
把(*)代入曲线C的方程可得:(1-
| 1 |
| 2 |
| ||
| 2 |
化为m2-(1+
| 3 |
根据参数的几何意义可得:|PA|•|PB|=m1m2=1.
故答案为:1.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
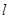 的参数方程为
的参数方程为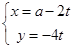 ,(
,(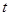 为参数),圆
为参数),圆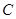 的参数方程为
的参数方程为 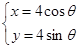 ,(
,(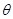 为参数).
为参数).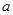 的取值范围.
的取值范围.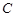 的参数方程为
的参数方程为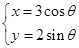 (
(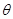 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线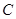 上的点按坐标变换
上的点按坐标变换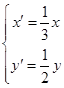 得到曲线
得到曲线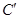 .
.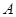 在曲线
在曲线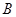
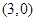 ,当点
,当点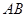 中点
中点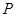 的轨迹方程.
的轨迹方程.