题目内容
 选修4-1:几何证明选讲
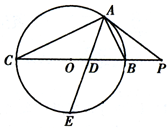
选修4-1:几何证明选讲如图所示,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠BAC的平分线与BC和⊙O分别交于点D和E.
(Ⅰ)求证:
| AB |
| AC |
| PA |
| PC |
(Ⅱ)求AD•AE的值.
分析:( I)直接根据∠PAB=∠ACP以及∠P公用,得到△PAB∽△PCA,进而求出结论;
( II)先根据切割线定理得到PA2=PB•PC;结合第一问的结论以及勾股定理求出AC=6
,AB=3
;再结合条件得到△ACE∽△ADB,进而求出结果.
( II)先根据切割线定理得到PA2=PB•PC;结合第一问的结论以及勾股定理求出AC=6
| 5 |
| 5 |
解答: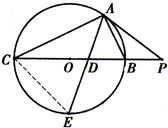 解:( I)∵PA为⊙O的切线,
解:( I)∵PA为⊙O的切线,
∴∠PAB=∠ACP,…(1分)
又∠P公用,∴△PAB∽△PCA.…(2分)
∴
=
.…(3分)
( II)∵PA为⊙O的切线,PBC是过点O的割线,
∴PA2=PB•PC.…(5分)
又∵PA=10,PB=5,∴PC=20,BC=15.…(6分)
由( I)知,
=
=
,
∵BC是⊙O的直径,
∴∠CAB=90°.
∴AC2+AB2=BC2=225,
∴AC=6
,AB=3
…(7分)
连接CE,则∠ABC=∠E,…(8分)
又∠CAE=∠EAB,
∴△ACE∽△ADB,
∴
=
…(9分)
∴AD•AE=AB•AC=3
×6
=90.…(10分)
 解:( I)∵PA为⊙O的切线,
解:( I)∵PA为⊙O的切线,∴∠PAB=∠ACP,…(1分)
又∠P公用,∴△PAB∽△PCA.…(2分)
∴
| AB |
| AC |
| PA |
| PC |
( II)∵PA为⊙O的切线,PBC是过点O的割线,
∴PA2=PB•PC.…(5分)
又∵PA=10,PB=5,∴PC=20,BC=15.…(6分)
由( I)知,
| AB |
| AC |
| PA |
| PC |
| 1 |
| 2 |
∵BC是⊙O的直径,
∴∠CAB=90°.
∴AC2+AB2=BC2=225,
∴AC=6
| 5 |
| 5 |
连接CE,则∠ABC=∠E,…(8分)
又∠CAE=∠EAB,
∴△ACE∽△ADB,
∴
| AB |
| AE |
| AD |
| AC |
∴AD•AE=AB•AC=3
| 5 |
| 5 |
点评:本题主要考查与圆有关的比例线段、相似三角形的判定及切线性质的应用.解决本题第一问的关键在于先由切线PA得到∠PAB=∠ACP.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲