题目内容
设M是弧度为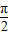 的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.
的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.(1)若
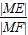 =1时,试问x的值为多少?
=1时,试问x的值为多少?(2)求
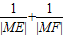 的取值范围.
的取值范围.
【答案】分析:(1)当 =1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,利用几何性质即可求出x的值;
=1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,利用几何性质即可求出x的值;
(2)在三角形OEM中,利用正弦定理列出关系式,表示出|EM|,同理表示出|FM|,代入所求式子中,利用两角和与差的正弦函数公式化为一个角的正弦函数,由x的范围求出这个角的范围,利用正弦函数的图象与性质化简求出范围.
解答:解:(1)当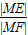 =1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,
=1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,
则由几何性质易知x=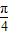 ;
;
(2)在三角形OEM中由正弦定理可知: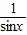 =
=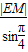 ,得|EM|=
,得|EM|=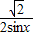 ,x∈(0,
,x∈(0,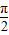 ),
),
同理在三角形OFM中由正弦定理可知:|FM|=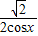 ,x∈(0,
,x∈(0,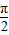 ),
),
从而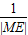 +
+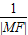 =
=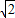 sinx+
sinx+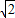 cosx=2sin(x+
cosx=2sin(x+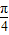 ),
),
∵x∈(0,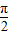 ),∴x+
),∴x+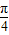 ∈(
∈(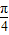 ,
,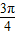 ),即有sin(x+
),即有sin(x+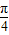 )∈(
)∈(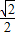 ,1],
,1],
则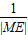 +
+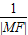 ∈(
∈(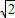 ,2].
,2].
点评:此题考查了正弦定理,两角和与差的正弦函数公式,以及正弦函数的定义域与值域,熟练掌握正弦定理是解本题的关键.
 =1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,利用几何性质即可求出x的值;
=1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,利用几何性质即可求出x的值;(2)在三角形OEM中,利用正弦定理列出关系式,表示出|EM|,同理表示出|FM|,代入所求式子中,利用两角和与差的正弦函数公式化为一个角的正弦函数,由x的范围求出这个角的范围,利用正弦函数的图象与性质化简求出范围.
解答:解:(1)当
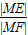 =1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,
=1时,即M为EF的中点,又M是∠AOB的角平分线上的一点,则由几何性质易知x=
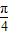 ;
;(2)在三角形OEM中由正弦定理可知:
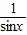 =
=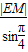 ,得|EM|=
,得|EM|=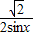 ,x∈(0,
,x∈(0,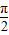 ),
),同理在三角形OFM中由正弦定理可知:|FM|=
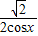 ,x∈(0,
,x∈(0,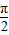 ),
),从而
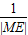 +
+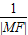 =
=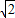 sinx+
sinx+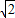 cosx=2sin(x+
cosx=2sin(x+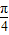 ),
),∵x∈(0,
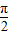 ),∴x+
),∴x+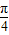 ∈(
∈(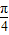 ,
,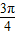 ),即有sin(x+
),即有sin(x+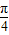 )∈(
)∈(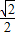 ,1],
,1],则
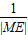 +
+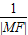 ∈(
∈(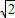 ,2].
,2].点评:此题考查了正弦定理,两角和与差的正弦函数公式,以及正弦函数的定义域与值域,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目