题目内容
已知椭圆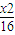 +
+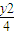 =1的左右焦点分别为F1与F2,点P在直线l:x-
=1的左右焦点分别为F1与F2,点P在直线l:x-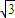 y+8+2
y+8+2 =0上.当∠F1PF2取最大值时,
=0上.当∠F1PF2取最大值时,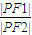 的比值为 .
的比值为 .
【答案】分析:先根据椭圆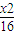 +
+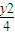 =1的方程得出其左右焦点分别为F1(-2
=1的方程得出其左右焦点分别为F1(-2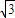 ,0)、与F2(2
,0)、与F2(2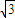 ,0).如图,根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2的圆与直线l 相切,求出圆心坐标,再利用相似三角形的知识得出
,0).如图,根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2的圆与直线l 相切,求出圆心坐标,再利用相似三角形的知识得出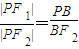 ,最后利用相似比即可求出答案.
,最后利用相似比即可求出答案.
解答: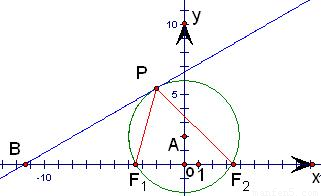 解:椭圆
解:椭圆 +
+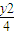 =1的左右焦点分别为F1(-2
=1的左右焦点分别为F1(-2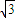 ,0)、与F2(2
,0)、与F2(2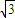 ,0).
,0).
如图,根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2,的圆与直线l 相切,此时圆心在y轴上,坐标为A(0,2),
在直线l:x-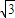 y+8+2
y+8+2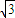 =0中令y=0得B的坐标:
=0中令y=0得B的坐标:
B(-8-2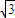 ,0),
,0),
在三角形BPF1和三角形BF2P中,∠BPF1=∠BF2P,
∴△BPF1∽△BF2P,
∴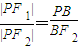 =
=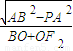 =
=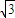 -1.
-1.
故答案为: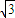 -1.
-1.
点评:本小题主要考查直线与圆锥曲线的关系、直线与圆的位置关系、圆的切线等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
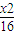 +
+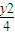 =1的方程得出其左右焦点分别为F1(-2
=1的方程得出其左右焦点分别为F1(-2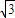 ,0)、与F2(2
,0)、与F2(2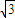 ,0).如图,根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2的圆与直线l 相切,求出圆心坐标,再利用相似三角形的知识得出
,0).如图,根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2的圆与直线l 相切,求出圆心坐标,再利用相似三角形的知识得出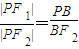 ,最后利用相似比即可求出答案.
,最后利用相似比即可求出答案.解答:
 解:椭圆
解:椭圆 +
+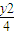 =1的左右焦点分别为F1(-2
=1的左右焦点分别为F1(-2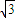 ,0)、与F2(2
,0)、与F2(2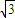 ,0).
,0).如图,根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2,的圆与直线l 相切,此时圆心在y轴上,坐标为A(0,2),
在直线l:x-
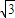 y+8+2
y+8+2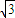 =0中令y=0得B的坐标:
=0中令y=0得B的坐标:B(-8-2
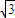 ,0),
,0),在三角形BPF1和三角形BF2P中,∠BPF1=∠BF2P,
∴△BPF1∽△BF2P,
∴
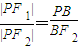 =
=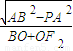 =
=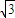 -1.
-1.故答案为:
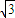 -1.
-1.点评:本小题主要考查直线与圆锥曲线的关系、直线与圆的位置关系、圆的切线等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
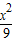 +
+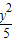 =1的左右焦点为F1、F2,P为椭圆上一点,O是坐标原点,M是PF1的中点,若|PF1|=4,则|OM|= .
=1的左右焦点为F1、F2,P为椭圆上一点,O是坐标原点,M是PF1的中点,若|PF1|=4,则|OM|= .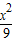 +
+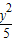 =1的左右焦点为F1、F2,P为椭圆上一点,O是坐标原点,M是PF1的中点,若|PF1|=4,则|OM|= .
=1的左右焦点为F1、F2,P为椭圆上一点,O是坐标原点,M是PF1的中点,若|PF1|=4,则|OM|= . +
+ =1的左右焦点分别为F1与F2,点P在直线l:x-
=1的左右焦点分别为F1与F2,点P在直线l:x- y+8+2
y+8+2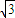 =0上.当∠F1PF2取最大值时,
=0上.当∠F1PF2取最大值时,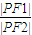 的比值为 .
的比值为 .