题目内容
在△ABC中,边AC=1,AB=2,角A=| 2π |
| 3 |
| AP |
| AB |
| AC |
分析:建立坐标系,用坐标表示向量,求出点P的坐标,代入
=λ
+μ
,求出λ、μ的值,即得结果.
| AP |
| AB |
| AC |
解答:解:建立坐标系,如图,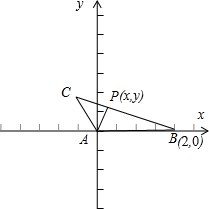 ;
;
设点P(x,y),则
=(x,y),
∵
=(2,0),|
|=1,∠CAB=
,∴
=(-
,
);
∴
=
-
=(-
,
);
又∵
⊥
,∴-
x+
y=0①;
与
共线,∴
(x-2)-(-
y)=0②;
由①②组成方程组,解得x=
,y=
,
∴
=(
,
);
又∵
=λ
+μ
,
∴(
,
)=λ(2,0)+μ(-
,
)=(2λ-
μ,
μ),
即
,
解得
,
∴λμ=
×
=
;
故答案为:
.
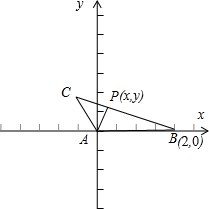 ;
;设点P(x,y),则
| AP |
∵
| AB |
| AC |
| 2π |
| 3 |
| AC |
| 1 |
| 2 |
| ||
| 2 |
∴
| BC |
| AC |
| AB |
| 5 |
| 2 |
| ||
| 2 |
又∵
| AP |
| BC |
| 5 |
| 2 |
| ||
| 2 |
| BP |
| BC |
| ||
| 2 |
| 5 |
| 2 |
由①②组成方程组,解得x=
| 3 |
| 14 |
5
| ||
| 14 |
∴
| AP |
| 3 |
| 14 |
5
| ||
| 14 |
又∵
| AP |
| AB |
| AC |
∴(
| 3 |
| 14 |
5
| ||
| 14 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
即
|
解得
|
∴λμ=
| 2 |
| 7 |
| 5 |
| 7 |
| 10 |
| 49 |
故答案为:
| 10 |
| 49 |
点评:本题考查了平面向量的线性运算以及向量垂直和共线等问题,是综合性题目.

练习册系列答案
相关题目
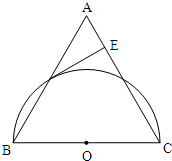 如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.则
如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.则