题目内容
(本小题满分14分)数列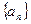 中,
中,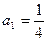 ;
;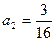 ,对任意的
,对任意的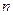 为正整数都有
为正整数都有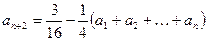 。
。
(1)求证: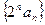 是等差数列;
是等差数列;
(2)求出
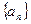 的通项公式
的通项公式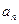 ;
;
(3)若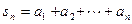 (
(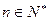 ),是否存在实数
),是否存在实数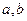 使得
使得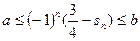 对任意的
对任意的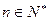 恒成立?若存在,找出
恒成立?若存在,找出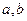 ;若不存在,请说明理由。
;若不存在,请说明理由。
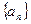 中,
中,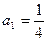 ;
;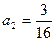 ,对任意的
,对任意的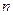 为正整数都有
为正整数都有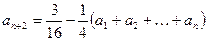 。
。(1)求证:
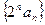 是等差数列;
是等差数列;(2)求出

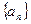 的通项公式
的通项公式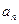 ;
;(3)若
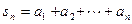 (
(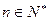 ),是否存在实数
),是否存在实数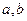 使得
使得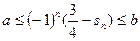 对任意的
对任意的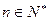 恒成立?若存在,找出
恒成立?若存在,找出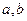 ;若不存在,请说明理由。
;若不存在,请说明理由。解:(1)由题意可知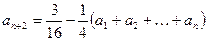

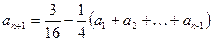 (
(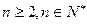 )两式相减可得
)两式相减可得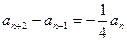
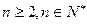 ,又
,又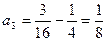
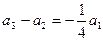 也成立,所以
也成立,所以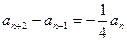 ,
,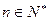 ,等式两边同乘
,等式两边同乘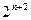 可得
可得
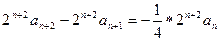 ,所以
,所以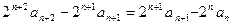
所以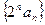 是等差数列。…………………6分
是等差数列。…………………6分
(2)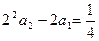 ,
,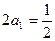 ,所以
,所以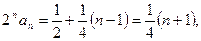
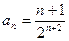 (
(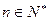 ) ………………8分
) ………………8分
(3)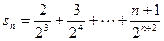 ,
,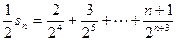
两式相减可得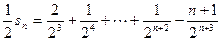
所以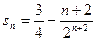 (
(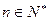 )
)
所以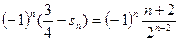
各项为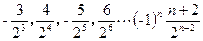
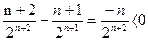 恒成立,所以上述数列中奇数项从
恒成立,所以上述数列中奇数项从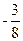 递增趋向于零,偶数项从
递增趋向于零,偶数项从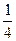 递减趋向于零,所以存在
递减趋向于零,所以存在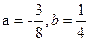 使得
使得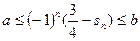 对任意的
对任意的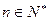 恒成立。…………………14分
恒成立。…………………14分
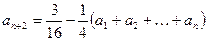

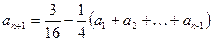 (
(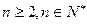 )两式相减可得
)两式相减可得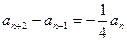
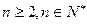 ,又
,又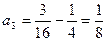
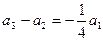 也成立,所以
也成立,所以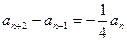 ,
,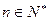 ,等式两边同乘
,等式两边同乘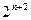 可得
可得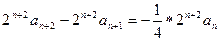 ,所以
,所以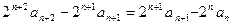
所以
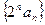 是等差数列。…………………6分
是等差数列。…………………6分(2)
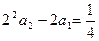 ,
,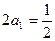 ,所以
,所以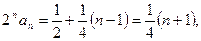
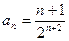 (
(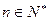 ) ………………8分
) ………………8分(3)
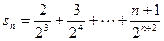 ,
,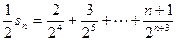
两式相减可得
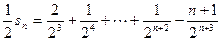
所以
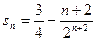 (
(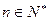 )
)所以
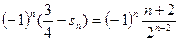
各项为
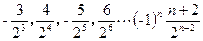
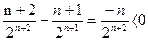 恒成立,所以上述数列中奇数项从
恒成立,所以上述数列中奇数项从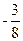 递增趋向于零,偶数项从
递增趋向于零,偶数项从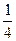 递减趋向于零,所以存在
递减趋向于零,所以存在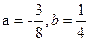 使得
使得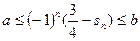 对任意的
对任意的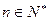 恒成立。…………………14分
恒成立。…………………14分略

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
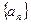 满足:
满足: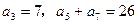 ,
,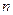 项和为
项和为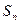 。
。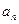 及
及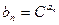 (其中
(其中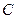 为常数,且
为常数,且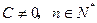 ),求证数列
),求证数列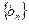 为等比数列。
为等比数列。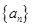 满足
满足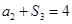 ,
,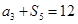 ,则
,则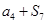 的值是( )
的值是( )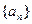 和
和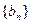 满足:
满足: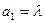 ,
,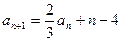 ,
,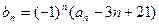 ,其中
,其中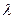 为实数,
为实数,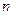 为正整数。
为正整数。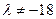 时,数列
时,数列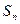 为数列
为数列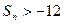 ?若存在,求
?若存在,求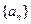 ,
,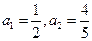 ,且对满足
,且对满足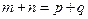 的任意正整
的任意正整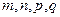 都有
都有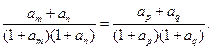
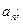
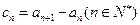 ,设数列
,设数列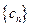 的前
的前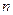 项和为
项和为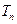 ,求证:对任意正整数
,求证:对任意正整数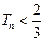 。
。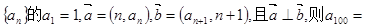 ( )
( )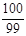
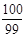
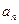 }的前
}的前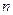 项和
项和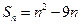 ,若它的第
,若它的第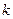 项满足
项满足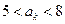 ,则
,则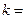 .
.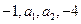 成等差数列,
成等差数列, 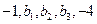 成等比数列,则
成等比数列,则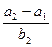 的值为________.
的值为________.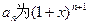 的展开式中含
的展开式中含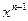 项的系数,则数列
项的系数,则数列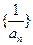 的前
的前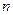 项和为
项和为