题目内容
【题目】已知数列{an}满足a1=1，a2=3，若|an+1﹣an|=2n（n∈N*），且{a2n﹣1}是递增数列、{a2n}是递减数列，则 
= ．
【答案】﹣ 
【解析】解：∵a1=1，a2=3，|an+1﹣an|=2n（n∈N*）， ∴a3﹣a2=±22 ，
又{a2n﹣1}是递增数列、{a2n}是递减数列，
∴a3﹣a2=4=22；
同理可得，a4﹣a3=﹣23 ，
a5﹣a4=24 ，
a6﹣a5=﹣25 ，
…，
a2n﹣1﹣a2n﹣2=22n﹣2 ，
a2n﹣a2n﹣1=﹣22n﹣1 ，
∴a2n=（a2n﹣a2n﹣1）+（a2n﹣1﹣a2n﹣2）+…+（a3﹣a2）+（a2﹣a1）+a1=1+2+（22﹣23+24﹣…+22n﹣2﹣22n﹣1）=3+ 
= 
﹣ 
22n﹣2= ﹣ 
22n；
∴a2n﹣1=a2n+22n﹣1= + 
22n；
∴则 
= 
= 
=﹣ ．
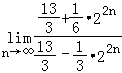所以答案是：﹣ ．
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案【题目】某地区2009年至2015年农村居民家庭人均纯收入y（单位：千元）的数据如表：
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
附：回归直线的斜率和截距的最小二乘估计公式分别为： 
． 
．
参考数据：（﹣3）×（﹣1.4）+（﹣2）×（﹣1）+（﹣1）×（﹣0.7）+1×0.5+2×0.9+3×1.6=14．
（1）求y关于t的线性回归方程；
（2）利用（1）中的回归方程，分析2009年至2015年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2017年农村居民家庭人均纯收入．
【题目】已知数列{an}是公差为2的等差数列，数列{bn}满足 
，若n∈N*时，anbn+1﹣bn+1=nbn ．
（Ⅰ）求{bn}的通项公式；
（Ⅱ）设cn=anbn ， 求{cn}的前n项和Sn ．
【题目】为了解市民在购买食物时看营养说明与性别的关系，现在社会上随机询问了100名市民，得到如下2×2列联表：
（1）是否有95%的把握认为：“性别与读营养说明有关系”，并说明理由；
（2）把频率当概率，若从社会上的男性市民中随机抽取3位，记这3位中读营养说明的人数为ξ，求随机变量ξ的分布列和数学期望E（ξ）．
男性 | 女性 | 总计 | |
读营养说明 | 40 | 20 | 60 |
不读营养说明 | 20 | 20 | 40 |
总计 | 60 | 40 | 100 |
参考公式和数据： 
P（K2≥k0） | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
