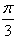题目内容
定义运算:,若将函数f(x)=
的图象向左平移m(m>0)个单位长度后,所得图象对应的函数为偶函数,则m的最小值是( )
|
分析:先用行列式展开法则求出f(x),再由函数的平移公式能够得到f(x+m),然后由偶函数的性质求出m的最小值.
解答:解:f(x)=
=
cosx-sinx=2cos(x+
),
图象向左平移m(m>0)个单位,
得f(x+m)=2cos(x+m+
),
则当n取得最小值
π时,函数为偶函数.
故选B.
|
| 3 |
| π |
| 6 |
图象向左平移m(m>0)个单位,
得f(x+m)=2cos(x+m+
| π |
| 6 |
则当n取得最小值
| 5 |
| 6 |
故选B.
点评:本题考查二阶行列式的展开法则,解题时要注意函数的平移和偶函数的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
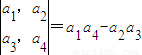 .若将函数
.若将函数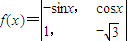 的图象向左平移m(m>0)个单位后,所得图象对应的函数为奇函数,则m的最小值是( )
的图象向左平移m(m>0)个单位后,所得图象对应的函数为奇函数,则m的最小值是( )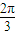

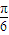

 .若将函数
.若将函数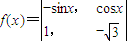 的图象向左平移m(m>0)个单位后,所得图象对应的函数为奇函数,则m的最小值是( )
的图象向左平移m(m>0)个单位后,所得图象对应的函数为奇函数,则m的最小值是( )
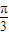

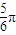
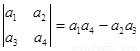 ,若将函数
,若将函数 的图象向左平移
的图象向左平移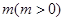 个单位长度后,所得图象对应的函数为偶函数,则m的最小值是( )
个单位长度后,所得图象对应的函数为偶函数,则m的最小值是( ) B.
B. C.
C.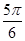 D.
D.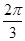
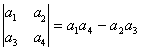 。若将函数f(x)=
。若将函数f(x)=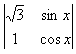 的图象向左平移m(m>0)个单位长度后,所得图象对应的函数为偶函数,则m的最小值是
的图象向左平移m(m>0)个单位长度后,所得图象对应的函数为偶函数,则m的最小值是