题目内容
在半径为2的圆内随机地取一点 ,以点
,以点 为中点做一条弦
为中点做一条弦 ,求弦
,求弦 长超过圆内接正三角形的边长概率是多少
长超过圆内接正三角形的边长概率是多少
A. | B.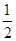 | C. | D. |
C
解析试题分析:由题意可得:符合条件的点必须在内接等边三角形的内切圆内,理由如下:因为两圆的圆心相同,大圆的半径为1,故内接正三角形的边长为

故内接等边三角形的内切圆半径为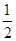 ,故所求的概率为
,故所求的概率为 ,故选C
,故选C
考点:本题考查了几何概型的求解
点评:此类几何概型问题,找到各自的度量是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法:
①正态分布 在区间
在区间 内取值的概率小于0.5;
内取值的概率小于0.5;
②正态曲线在 一定时,
一定时, 越小,曲线越“矮胖”;
越小,曲线越“矮胖”;
③若随机变量 ,且
,且 ,则
,则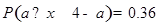
其中正确的命题有( )
| A.①② | B.② | C.①③ | D.③ |
设随机变量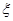 服从正态分布
服从正态分布 .若
.若 ,则
,则 的值为( )
的值为( )
A. | B. | C.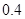 | D.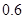 |
今年十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:性别与对景区的服务是否满意 单位:名
| | 男 | 女 | 总计 |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;
(3)根据以上列联表,问有多大把握认为“游客性别与对景区的服务满意”有关.
在区间 内随机取两个数分别记为
内随机取两个数分别记为 ,则使得函数
,则使得函数 有零点的概率为( )
有零点的概率为( )
A. | B. | C. | D. |
已知随机变量 服从正态分布
服从正态分布 ,且
,且 ,则
,则
A. | B. | C. | D. |
 的线段
的线段 上任取一点
上任取一点 现作一矩形,领边长分别等于线段
现作一矩形,领边长分别等于线段 的长,则该矩形面积小于
的长,则该矩形面积小于 的概率为( )
的概率为( )
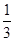
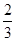

 表示的平面区域为D,在区域D内随机取一点,则此点到坐标原点的距离大于1的概率为
表示的平面区域为D,在区域D内随机取一点,则此点到坐标原点的距离大于1的概率为


