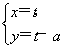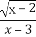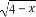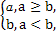题目内容
已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )
(A) ,2 (B)
,2 (B) ,4 (C)
,4 (C)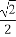 ,
,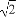 (D)
(D) ,4
,4
A
【解析】f(x)=|log2x|=
则函数f(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
又m<n且f(m)=f(n),则0<m<1,n>1,
∴0<m2<m<1,
∴f(m2)>f(m)=f(n),
即函数f(x)在区间[m2,n]上的最大值为f(m2).
由题意知f(m2)=2,即-log2m2=2,
∴m=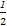 ,由f(m)=f(n)得-log2
,由f(m)=f(n)得-log2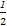 =log2n,∴n=2.
=log2n,∴n=2.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目