题目内容
已知椭圆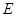 :
: 的离心率为
的离心率为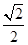 ,且过点
,且过点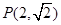 ,设椭圆的右准线
,设椭圆的右准线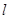 与
与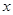 轴的交点为
轴的交点为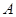 ,椭圆的上顶点为
,椭圆的上顶点为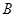 ,直线
,直线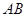 被以原点为圆心的圆
被以原点为圆心的圆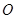 所截得的弦长为
所截得的弦长为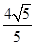 .
.
⑴求椭圆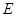 的方程及圆
的方程及圆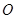 的方程;
的方程;
⑵若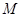 是准线
是准线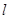 上纵坐标为
上纵坐标为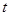 的点,求证:存在一个异于
的点,求证:存在一个异于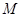 的点
的点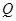 ,对于圆
,对于圆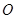 上任意一点
上任意一点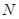 ,有
,有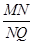 为定值;且当
为定值;且当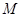 在直线
在直线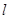 上运动时,点
上运动时,点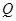 在一个定圆上.
在一个定圆上.
【答案】
⑴椭圆方程: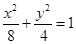 圆的方程:
圆的方程: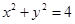
⑵定值为: ,
,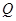 在圆心
在圆心 ,半径为
,半径为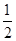 的定圆上
的定圆上
【解析】略

练习册系列答案
相关题目
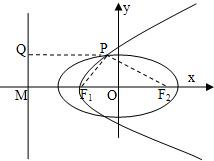 已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若
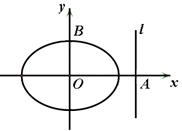
已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若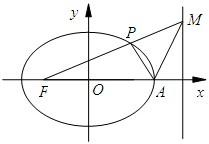 如图,在平面直角坐标系xOy中,椭圆C:
如图,在平面直角坐标系xOy中,椭圆C: