题目内容
已知实数x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则
的取值范围是( )
| (a1+a2)2 |
| b1b2 |
| A、[4,+∞) |
| B、(-∞,-4]∪[4,+∞) |
| C、(-∞,0]∪[4,+∞) |
| D、不能确定 |
分析:利用实数x,a1,a2,y成等差数列,实数x,b1,b2,y成等比数列,可得x+y=a1+a2,xy=b1b2,利用基本不等式,即可求得结论,注意讨论xy的符号.
解答:解:∵实数x,a1,a2,y成等差数列,实数x,b1,b2,y成等比数列,
∴x+y=a1+a2,xy=b1b2,
则
=
=
=
+
+2.
当xy>0时,
=
=
=
+
+2≥2
+2=4,当且仅当x=y时取等号
当xy<0时,
=
=
=
+
+2≤-2
+2=0,当且仅当x=y时取等号
综上所述,
的取值范围是(-∞,0]∪[4,+∞).
故选C.
∴x+y=a1+a2,xy=b1b2,
则
| (a1+a2)2 |
| b1b2 |
| (x+y)2 |
| xy |
| x2+y2+2xy |
| xy |
| x |
| y |
| y |
| x |
当xy>0时,
| (a1+a2)2 |
| b1b2 |
| (x+y)2 |
| xy |
| x2+y2+2xy |
| xy |
| x |
| y |
| y |
| x |
|
当xy<0时,
| (a1+a2)2 |
| b1b2 |
| (x+y)2 |
| xy |
| x2+y2+2xy |
| xy |
| x |
| y |
| y |
| x |
|
综上所述,
| (a1+a2)2 |
| b1b2 |
故选C.
点评:本题考查数列的性质和应用,解题时要注意均值不等式的合理运用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
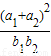 的取值范围是( )
的取值范围是( )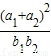 的取值范围是( )
的取值范围是( )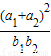 的取值范围是( )
的取值范围是( )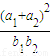 的取值范围是( )
的取值范围是( )