题目内容
已知动点A,B分别在x轴、y轴上,且满足|AB|=2,点P在线段AB上,且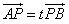 (t是不为零的常数)。设点P的轨迹为曲线C。
(t是不为零的常数)。设点P的轨迹为曲线C。
(1)求点P的轨迹方程;
(2)若t=2,点M,N是C上关于原点对称的两个动点(M,N不在坐标轴上),点Q(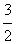 ,3),求△QMN的面积S的最大值。
,3),求△QMN的面积S的最大值。
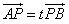 (t是不为零的常数)。设点P的轨迹为曲线C。
(t是不为零的常数)。设点P的轨迹为曲线C。(1)求点P的轨迹方程;
(2)若t=2,点M,N是C上关于原点对称的两个动点(M,N不在坐标轴上),点Q(
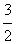 ,3),求△QMN的面积S的最大值。
,3),求△QMN的面积S的最大值。 解:(1)设A(a,0),B(0,b),P(x,y),由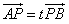 得
得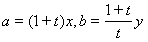 ,
,
由|AB|=2,
得点P轨迹方程为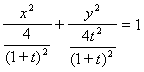 。
。
(2)当t=2时,C的方程为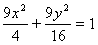 ,
,
设直线方程为y=kx与C方程联立得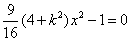 ,
,
易得△>0,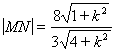 ,
,
点Q到直线的距离为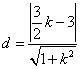 ,
,
得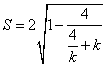 ,
,
所以,当且仅当k=-2时,S有最大值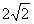 。
。
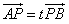 得
得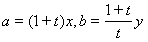 ,
,由|AB|=2,
得点P轨迹方程为
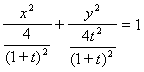 。
。(2)当t=2时,C的方程为
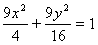 ,
,设直线方程为y=kx与C方程联立得
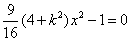 ,
,易得△>0,
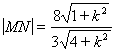 ,
,点Q到直线的距离为
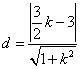 ,
,得
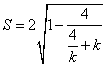 ,
,所以,当且仅当k=-2时,S有最大值
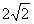 。
。 
练习册系列答案
相关题目
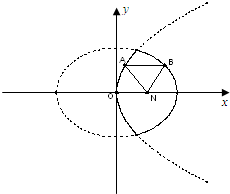 [理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆
[理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆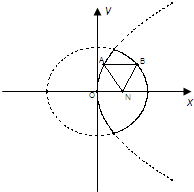 已知动点A、B分别在图中抛物线y2=4x及椭圆
已知动点A、B分别在图中抛物线y2=4x及椭圆 已知动点A、B分别在图中抛物线y2=4x及椭圆
已知动点A、B分别在图中抛物线y2=4x及椭圆 及椭圆
及椭圆 的实线上运动,若
的实线上运动,若 ∥
∥ 轴,点N的坐标
轴,点N的坐标 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.