题目内容
设f（x）=|lgx|，若a≠b，且f（a）=f（b），则a•b=
1
1
．分析：数形结合法即可解得．
解答：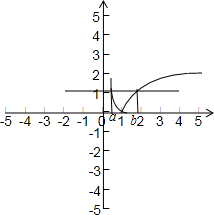
解：因为a≠b，不妨设a＜b，如图所示：则0＜a＜1，b＞1，
由f（a）=f（b），得|lga|=|lgb|，即-lga=lgb，所以lga+lgb=0，lgab=0，所以ab=1．
故答案为：1．
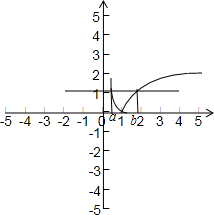解：因为a≠b，不妨设a＜b，如图所示：则0＜a＜1，b＞1，由f（a）=f（b），得|lga|=|lgb|，即-lga=lgb，所以lga+lgb=0，lgab=0，所以ab=1．
故答案为：1．
点评：本题考查了对数函数的图象与性质，本题中要充分体会数形结合的强大威力．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
相关题目