题目内容
已知下列结论:①已知a,b,c为实数,则“b2=ac”是“a,b,c成等比数列”的充要条件;
②满足条件
 的△ABC的个数为2;
的△ABC的个数为2;③若两向量
 的夹角为钝角,则实数λ的取值范围为
的夹角为钝角,则实数λ的取值范围为 ;
;④若x为三角形中的最小内角,则函数y=sinx+cosx的值域是
 ;
; ⑤某厂去年12月份产值是同年一月份产值的m倍,则该厂去年的月平均增长率为
 ;
;则其中正确结论的序号是 .
【答案】分析:①根据等比数列的定义,可以判断①的真假;
②先利用正弦定理求出sinB的值,然后根据大边对大角的原理可求出角B,从而确定满足条件的三角形的个数.
③由向量的数量积定义公式,可知两个向量数量积大于-1小于0,即数量积小于0 且两向量不为反向向量.
④由x为三角形中的最小内角,可得0<x≤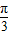 而y=sinx+cosx=
而y=sinx+cosx= sin(x+
sin(x+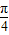 ),结合已知所求的x的范围可求y的范围.
),结合已知所求的x的范围可求y的范围.
⑤先假设增长率为p,再根据条件可得(1+p)11=m,从而可解出p值.
解答:解:对于①:a、b、c成等比数列的充要条件是b2=ac(a•b•c≠0),故①为假命题;
②:∵a=3,b=2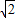 ,A=45°,
,A=45°,
∴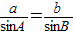 即
即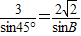 ,∴sinB=
,∴sinB= ,∵a>b,∴A>B,则B有1解,
,∵a>b,∴A>B,则B有1解,
满足条件的三角形的个数为1,故②为假命题;
③由 •
•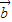 =(-2,1)•(λ,-1)=-2λ-1<0,得λ>-
=(-2,1)•(λ,-1)=-2λ-1<0,得λ>- ,若为反向向量,则λ=2
,若为反向向量,则λ=2
所以实数λ的取值范围是λ>- ,且λ≠2,即λ∈(-
,且λ≠2,即λ∈(- ,2)∪(2,+∞)
,2)∪(2,+∞)
故实数λ的取值范围为:(- ,2)∪(2,+∞).故③为假命题;
,2)∪(2,+∞).故③为假命题;
④因为x为三角形中的最小内角,
所以0<x≤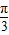 ,y=sinx+cosx=
,y=sinx+cosx=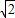 sin(x+
sin(x+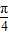 )
)
∴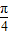 <
<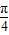 +x≤
+x≤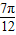 ,
,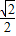 <sin(x+
<sin(x+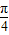 )≤1
)≤1
∴1<y≤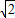 .故④为真命题;
.故④为真命题;
⑤由题意,设该厂去年产值的月平均增长率为p,则(1+p)11=m,∴p=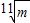 -1,故⑤为真命题;
-1,故⑤为真命题;
故答案为:④⑤.
点评:本题考查的知识点是命题的真假判断与应用,其中熟练掌握解三角形、等比数列的定义、正弦函数的部分图象的性质、偶函数的定义及性质等基础知识点是解答本题的关键.
②先利用正弦定理求出sinB的值,然后根据大边对大角的原理可求出角B,从而确定满足条件的三角形的个数.
③由向量的数量积定义公式,可知两个向量数量积大于-1小于0,即数量积小于0 且两向量不为反向向量.
④由x为三角形中的最小内角,可得0<x≤
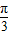 而y=sinx+cosx=
而y=sinx+cosx= sin(x+
sin(x+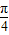 ),结合已知所求的x的范围可求y的范围.
),结合已知所求的x的范围可求y的范围.⑤先假设增长率为p,再根据条件可得(1+p)11=m,从而可解出p值.
解答:解:对于①:a、b、c成等比数列的充要条件是b2=ac(a•b•c≠0),故①为假命题;
②:∵a=3,b=2
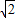 ,A=45°,
,A=45°,∴
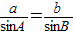 即
即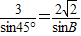 ,∴sinB=
,∴sinB= ,∵a>b,∴A>B,则B有1解,
,∵a>b,∴A>B,则B有1解,满足条件的三角形的个数为1,故②为假命题;
③由
 •
•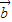 =(-2,1)•(λ,-1)=-2λ-1<0,得λ>-
=(-2,1)•(λ,-1)=-2λ-1<0,得λ>- ,若为反向向量,则λ=2
,若为反向向量,则λ=2所以实数λ的取值范围是λ>-
 ,且λ≠2,即λ∈(-
,且λ≠2,即λ∈(- ,2)∪(2,+∞)
,2)∪(2,+∞)故实数λ的取值范围为:(-
 ,2)∪(2,+∞).故③为假命题;
,2)∪(2,+∞).故③为假命题;④因为x为三角形中的最小内角,
所以0<x≤
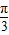 ,y=sinx+cosx=
,y=sinx+cosx=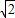 sin(x+
sin(x+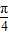 )
)∴
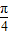 <
<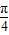 +x≤
+x≤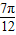 ,
,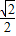 <sin(x+
<sin(x+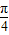 )≤1
)≤1∴1<y≤
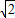 .故④为真命题;
.故④为真命题;⑤由题意,设该厂去年产值的月平均增长率为p,则(1+p)11=m,∴p=
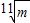 -1,故⑤为真命题;
-1,故⑤为真命题;故答案为:④⑤.
点评:本题考查的知识点是命题的真假判断与应用,其中熟练掌握解三角形、等比数列的定义、正弦函数的部分图象的性质、偶函数的定义及性质等基础知识点是解答本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 <0;
<0; 是共线的.
是共线的.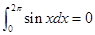 ;
; ,若
,若 ,则
,则 1
1 为定义在R上的可导函数,且
为定义在R上的可导函数,且 对于
对于 恒成立,则有
恒成立,则有 ,
,  ;
; 满足:(1)
满足:(1) ,(2)
,(2) (3)
(3) ,则
,则 =
=