题目内容
(本小题满分l2分)某市第一中学要用鲜花布置花圃中 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
(1)当 区域同时用红色鲜花时,求布置花圃的不同方法的种数;
区域同时用红色鲜花时,求布置花圃的不同方法的种数;
(2)求恰有两个区域用红色鲜花的概率;
(3)记 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量 的分布列及其数学期望.
的分布列及其数学期望.

【答案】
(1)36
(2)6/35
(3)
|
|
0 |
1 |
2 |
|
p |
6/35 |
23/35 |
6/35 |
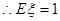
【解析】
解:因为(1)当A,D区域同时用红色鲜花时,其它区域不能用红色,因此
布置花圃的不同方法的种树为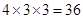 ………………..4分
………………..4分
(2)设m表示事件”恰有两个区域用红色鲜花”,当区域A,D同色时,共有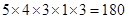
当区域A,D同色时,共有 ,因此所有基本事件总数有180+240=420种。………………..6分
,因此所有基本事件总数有180+240=420种。………………..6分
又因为A,D为红色时,共有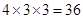 ,B,E为红色时,共有
,B,E为红色时,共有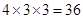 因此事件包含的事件总数为36+36=72种。
因此事件包含的事件总数为36+36=72种。
所以P(M)=72/420=6/35………………..8分
(3)随机变量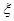 的分布列为
的分布列为
|
|
0 |
1 |
2 |
|
p |
6/35 |
23/35 |
6/35 |

练习册系列答案
相关题目
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线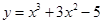 相切的直线方程.
相切的直线方程.