题目内容
在极坐标系中,点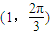 到圆ρ=2cosθ上动点的距离的最大值为 .
到圆ρ=2cosθ上动点的距离的最大值为 .
【答案】分析:把极坐标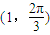 化为直角坐标是(-
化为直角坐标是(-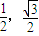 ),圆ρ=2cosθ化为(x-1)2+y2=1,由此能求出点到圆上的动点距离最大值.
),圆ρ=2cosθ化为(x-1)2+y2=1,由此能求出点到圆上的动点距离最大值.
解答:解:把极坐标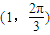 化为直角坐标:
化为直角坐标:
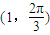 ⇒(cos
⇒(cos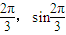 )⇒(-
)⇒(-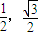 ),
),
圆ρ=2cosθ⇒ρ2=2cosθ⇒x2+y2=2x⇒(x-1)2+y2=1,
∴点到圆上的动点距离最大值为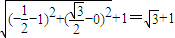 .
.
故答案为: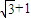 .
.
点评:本题考查极坐标的性质和应用,解题时要先把极坐标化成直角坐标,然后再用两点间距离公式进行求解.
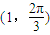 化为直角坐标是(-
化为直角坐标是(-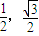 ),圆ρ=2cosθ化为(x-1)2+y2=1,由此能求出点到圆上的动点距离最大值.
),圆ρ=2cosθ化为(x-1)2+y2=1,由此能求出点到圆上的动点距离最大值.解答:解:把极坐标
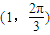 化为直角坐标:
化为直角坐标: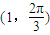 ⇒(cos
⇒(cos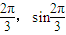 )⇒(-
)⇒(-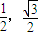 ),
),圆ρ=2cosθ⇒ρ2=2cosθ⇒x2+y2=2x⇒(x-1)2+y2=1,
∴点到圆上的动点距离最大值为
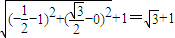 .
.故答案为:
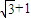 .
.点评:本题考查极坐标的性质和应用,解题时要先把极坐标化成直角坐标,然后再用两点间距离公式进行求解.

练习册系列答案
相关题目
在极坐标系中,点 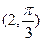 到圆
到圆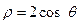 的圆心的距离为
的圆心的距离为
| A.2 | B. | C. | D.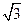 |
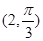 到圆
到圆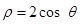 的圆心的距离为(
).
的圆心的距离为(
).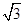 C.
C.
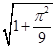 D
D
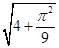
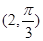 到圆
到圆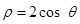 的圆心的距离为( )
的圆心的距离为( )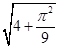 C.
C.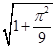 D.
D.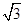
 到圆ρ=2cosθ的圆心的距离为
到圆ρ=2cosθ的圆心的距离为
 到圆
到圆 的圆心的距离为
的圆心的距离为 (C)
(C)
 (D)
(D) 