题目内容
设a、b分别是甲、乙各抛掷一枚骰子得到的点数.已知乙所得的点数为2,则方程x2+ax+b=0有两个不相等的实数根的概率为 .
【答案】分析:由题意可得b=2,由△=a2-4b=a2-8>0,可得 a=3,4,5,6,共有4种情况.而a的所有情况共有6种,
由此求得所求事件的概率.
解答:解:由题意可得b=2,由方程x2+ax+b=0有两个不相等的实数根可得△=a2-4b=a2-8>0,
即 a>2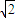 ,故 a=3,4,5,6,共有4种情况.而a的所有情况共有6种,
,故 a=3,4,5,6,共有4种情况.而a的所有情况共有6种,
故a>2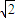 的概率为
的概率为 =
= ,
,
故答案为 .
.
点评:本题主要考查用列举法计算基本事件的个数,以及事件发生的概率,属于基础题.
由此求得所求事件的概率.
解答:解:由题意可得b=2,由方程x2+ax+b=0有两个不相等的实数根可得△=a2-4b=a2-8>0,
即 a>2
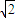 ,故 a=3,4,5,6,共有4种情况.而a的所有情况共有6种,
,故 a=3,4,5,6,共有4种情况.而a的所有情况共有6种,故a>2
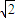 的概率为
的概率为 =
= ,
,故答案为
 .
.点评:本题主要考查用列举法计算基本事件的个数,以及事件发生的概率,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目