题目内容
已知三个正实数a、b、c满足a<b+c≤2a,b<a+c≤2b,则
的取值范围是( )
| b |
| a |
分析:根据题意,a轴为横轴,b轴为纵轴建立平面直角坐标系,画出可行域,利用
的几何意义即可求得结果.
| b |
| a |
解答:解根据题意知
画出可行域如图所示,
由
解得点M的坐标为(3c,2c),
由
解得点N的坐标为(2c,3c),
∴kOM <
< kON,即
<
<
故选C.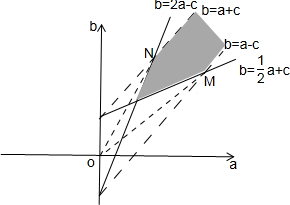
|
画出可行域如图所示,
由
|
由
|
∴kOM <
| b |
| a |
| 2 |
| 3 |
| b |
| a |
| 3 |
| 2 |
故选C.

点评:本题考查应用线性规划求解范围,准确画出可行域是解题的关键,利用
的几何意义求解是难点,属中档题.
| b |
| a |

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知三个正实数a、b、c,则下列三个数2a+
,b+
,c+
( )
| 1 |
| b |
| 1 |
| c |
| 1 |
| 2a |
| A、都大于2 |
| B、都小于2 |
| C、至少有一个小于2 |
| D、至少有一个不小于2 |
 ,
, ,
, ( )
( ) 的取值范围是
的取值范围是
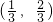
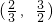
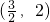
 的取值范围是( )
的取值范围是( )


