题目内容
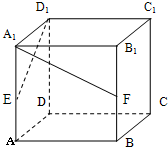
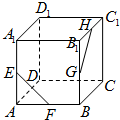
在正方体ABCD-A1B1C1D1中，AA1=a，E、F分别是BC、DC的中点，则AD1与EF所成的角的大小为______．
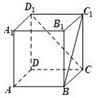
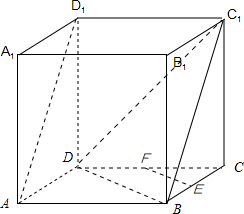
连接BD，BC1，DC1，如图所示：
由正方体的几何特征可得
EF∥BD，AD1∥BC1，
故∠DBC1或其补角即为AD1与EF所成的角
∵在△DBC1中，BD=BC1=DC1，
故∠DBC1=60°
故AD1与EF所成的角的大小为60°
故答案为：60°
由正方体的几何特征可得
EF∥BD，AD1∥BC1，
故∠DBC1或其补角即为AD1与EF所成的角
∵在△DBC1中，BD=BC1=DC1，
故∠DBC1=60°
故AD1与EF所成的角的大小为60°
故答案为：60°
练习册系列答案
相关题目
B
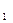的中点，P为AD上一动点，记
为异面直线PM与D
}
≤
≤
≤
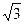，用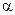
表示∠ASD，求
