题目内容
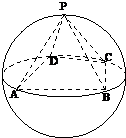 如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知
如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知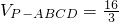 .
.
(1)求球O的表面积;
(2)设M为BC中点,求异面直线AM与PC所成角的大小.
解:(1)解:如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,PO⊥底面ABCD,PO=R,SABCD=2R2,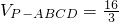 ,
,
所以 ,R=2,
,R=2,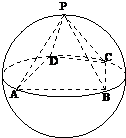
球O的表面积是16π
(2)以OP,OA,OB为x,y,z轴建立空间直角坐标系,则
P(0,0,2),A(2,0,0),B(0,2,0),C(-2,0,0),M(-1,1,0),
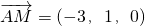 ,
,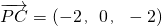 ,
,
所以
所以异面直线AM与PC所成角的余弦值为 .
.
所以异面直线AM与PC所成角的大小为 .
.
分析:(1)由题意可知,PO⊥平面ABCD,并且是半径,由体积求出半径,然后求出球的表面积.
(2)以OP,OA,OB为x,y,z轴建立空间直角坐标系,写出各点的坐标,进一步求出 的坐标,利用向量的数量积公式求出
的坐标,利用向量的数量积公式求出 的夹角余弦,得到异面直线AM与PC所成角的大小.
的夹角余弦,得到异面直线AM与PC所成角的大小.
点评:本题考查球的内接体问题,球的表面积、体积,考查学生空间想象能力,通过建立空间直角坐标系,将异面直线所成的角通过向量的数量积来解决.
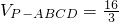 ,
,所以
 ,R=2,
,R=2,
球O的表面积是16π
(2)以OP,OA,OB为x,y,z轴建立空间直角坐标系,则
P(0,0,2),A(2,0,0),B(0,2,0),C(-2,0,0),M(-1,1,0),
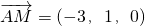 ,
,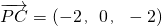 ,
,所以

所以异面直线AM与PC所成角的余弦值为
 .
.所以异面直线AM与PC所成角的大小为
 .
.分析:(1)由题意可知,PO⊥平面ABCD,并且是半径,由体积求出半径,然后求出球的表面积.
(2)以OP,OA,OB为x,y,z轴建立空间直角坐标系,写出各点的坐标,进一步求出
 的坐标,利用向量的数量积公式求出
的坐标,利用向量的数量积公式求出 的夹角余弦,得到异面直线AM与PC所成角的大小.
的夹角余弦,得到异面直线AM与PC所成角的大小.点评:本题考查球的内接体问题,球的表面积、体积,考查学生空间想象能力,通过建立空间直角坐标系,将异面直线所成的角通过向量的数量积来解决.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若
如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,若 如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
如图,正四棱锥P-ABCD的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( ) (2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知
(2008•上海一模)如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,且已知 如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心.
如图,正四棱锥P-ABCD中,PA=2,AB=1,M是侧棱PC的中点,O为底面正方形的中心. (2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )
(2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )