题目内容
(本题满分14分)设函数![]()
![]() .给出下列条件,条件A:
.给出下列条件,条件A: ![]() 在
在![]() 和
和![]() 处取得极值;条件
处取得极值;条件![]() :
: ![]()
(Ⅰ)在A条件下,求出实数![]() 的值;
的值;
(Ⅱ) 在A条件下,对于在![]() 上的任意
上的任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最小值;
的最小值;
(Ⅲ) 在![]() 条件下, 若
条件下, 若![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围.
的取值范围.
温馨提示:请将各题的答案写在答题纸上,同时选择题填涂答题卡
解:(Ⅰ)![]() ,定义域为
,定义域为![]()
∴![]() ………………1分
………………1分
![]() 在
在![]() 处取得极值,∴
处取得极值,∴![]() ………………2分
………………2分
即![]() 解得
解得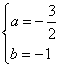 此时,
此时, ![]()
可看出![]() 且
且![]() 在
在![]() 和
和![]() 两侧均为异号,符合极值条件
两侧均为异号,符合极值条件
∴所求![]() 的值分别为
的值分别为![]() …………………4分
…………………4分
(Ⅱ) 对于在![]() 上的任意
上的任意![]() ,不等式
,不等式![]() 恒成立,只需
恒成立,只需![]()
由![]()
![]()
![]() ,
,
∴当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是单调递增
上是单调递增
当![]() 时;
时; ![]() ,故
,故![]() 在
在![]() 上单调递减
上单调递减
当![]() 时;
时; ![]() ,故
,故![]() 在
在![]() 上单调递增
上单调递增
∴![]() 是
是![]() 在
在![]() 上的极大值…………… 6分
上的极大值…………… 6分
而![]() ,
,![]() ………8分
………8分
∴ ![]() ∴
∴![]() 的取值范围为
的取值范围为![]() ,所以
,所以![]() 得最小值为
得最小值为![]() ……9分
……9分
(Ⅲ) 当![]() 时,
时,![]()
①当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增…………10分
上单调递增…………10分
②![]() 要使
要使![]() 在
在![]() 恒成立
恒成立
令![]() ,
,
则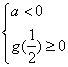 ,即
,即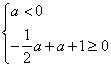 ,解得
,解得![]() ……………12分
……………12分
③![]() 要使
要使![]() 在
在![]() 恒成立
恒成立
令![]() ,
, 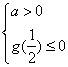 ,即
,即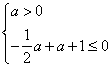 无解
无解
综上可知![]() 的取值范围为
的取值范围为![]() ……………………………14分
……………………………14分

练习册系列答案
相关题目
 的左、右焦点分别为F1与
的左、右焦点分别为F1与 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。 变成曲线
变成曲线 ,直线
,直线 与曲线
与曲线 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点) 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 满足
满足 ”
” 是集合M中的元素;
是集合M中的元素;
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。  .
. ,求函数
,求函数 的极值;
的极值; ,试确定
,试确定 的单调性;
的单调性; ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.