题目内容
在2009年“家电下乡”活动中,某品牌家电厂家从某地购买该品牌家电的用户中随机抽取20名用户进行满意度调查.设满意度最低为0,最高为10,抽查结果统计如下:| 满意度分组 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
| 用户数 | 1 | 2 | 4 | 5 | 8 |

(2)估计这20名用户满意度的中位数;
(3)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,现从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.
【答案】分析:(1)根据统计数据按规则作出频率分布直方图,横坐标是组距,纵坐标为
(2)从直方图中求中位数的估计值是要找出其左右两边小矩形的面积都是0.5的那个数,故可对各个小矩形的面积进行研究,找出等分矩形面积和的那个数.
(3)五个数中取两个的组合有10个,故共有10个基本事件,列举出这十个基本事件,对其中的两个数据做差,发现符号条件的事件包含的基本事件个数为7,由古典概率模型的求概率公式求出概率即可.
解答:解:(1)频率分布直方图如下:
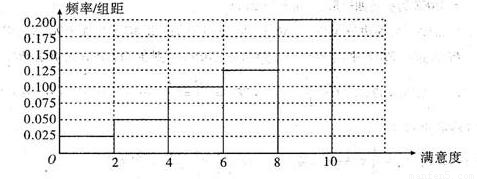
(2)各组的频率依次为:0.05,0.10,0.20,0.25,0.40,
∵0.05+0.10+0.20=0.35<0.50,而0.05+0.10+0.20+0.25=0.60>0.50
∴中位数在区间[6,8]内,设为x,则有
0.025*2+0.05*2+0.1*2+0.125*(x-6)=0.5,解得x=7.2即中位数为7.2
(3)6.5,7,7.5,7.5,7.9中取两个的基本事件有10个即
(6.5,7),(6.5,7.5),(6.5,7.5),(6.5,7.9),(7,7.5),(7,7.5),(7,7.9),(7.5,7.5),(7.5,9),(7.5,9),
其中满足|x-y|<1的有7个:(6.5,7),(7,7.5),(7,7.5),(7,7.9),(7.5,7.5),(7.5,9),(7.5,9)
∴|x-y|<1的概率为 .
.
点评:本题综合考查了数据图表统计的方法及古典概率模型求概率,是统计与概率中的一道很有代表性的综合题,也是这几年高考的热点题型.

(2)从直方图中求中位数的估计值是要找出其左右两边小矩形的面积都是0.5的那个数,故可对各个小矩形的面积进行研究,找出等分矩形面积和的那个数.
(3)五个数中取两个的组合有10个,故共有10个基本事件,列举出这十个基本事件,对其中的两个数据做差,发现符号条件的事件包含的基本事件个数为7,由古典概率模型的求概率公式求出概率即可.
解答:解:(1)频率分布直方图如下:

(2)各组的频率依次为:0.05,0.10,0.20,0.25,0.40,
∵0.05+0.10+0.20=0.35<0.50,而0.05+0.10+0.20+0.25=0.60>0.50
∴中位数在区间[6,8]内,设为x,则有
0.025*2+0.05*2+0.1*2+0.125*(x-6)=0.5,解得x=7.2即中位数为7.2
(3)6.5,7,7.5,7.5,7.9中取两个的基本事件有10个即
(6.5,7),(6.5,7.5),(6.5,7.5),(6.5,7.9),(7,7.5),(7,7.5),(7,7.9),(7.5,7.5),(7.5,9),(7.5,9),
其中满足|x-y|<1的有7个:(6.5,7),(7,7.5),(7,7.5),(7,7.9),(7.5,7.5),(7.5,9),(7.5,9)
∴|x-y|<1的概率为
 .
.点评:本题综合考查了数据图表统计的方法及古典概率模型求概率,是统计与概率中的一道很有代表性的综合题,也是这几年高考的热点题型.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在2009年“家电下乡”活动中,某品牌家电厂家从某地购买该品牌家电的用户中随机抽取20名用户进行满意度调查.设满意度最低为0,最高为10,抽查结果统计如下:
(1)成下列频率分布直方图;

(2)估计这20名用户满意度的中位数;
(3)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,现从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.
| 满意度分组 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
| 用户数 | 1 | 2 | 4 | 5 | 8 |

(2)估计这20名用户满意度的中位数;
(3)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,现从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.
在2009年“家电下乡”活动中,某品牌家电厂家从某地购买该品牌家电的用户中随机抽取20名用户进行满意度调查.设满意度最低为0,最高为10,抽查结果统计如下:
| 满意度分组 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
| 用户数 | 1 | 2 | 4 | 5 | 8 |
(2)估计这20名用户满意度的中位数;
(3)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,现从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.
在2009年“家电下乡”活动中,某品牌家电厂家从某地购买该品牌家电的用户中随机抽取20名用户进行满意度调查.设满意度最低为0,最高为10,抽查结果统计如下:
(1)成下列频率分布直方图;
(2)估计这20名用户满意度的中位数;
(3)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,现从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.
| 满意度分组 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
| 用户数 | 1 | 2 | 4 | 5 | 8 |

(2)估计这20名用户满意度的中位数;
(3)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,现从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.
在2009年“家电下乡”活动中,某品牌家电厂家从某地购买该品牌家电的用户中随机抽取20名用户进行满意度调查.设满意度最低为0,最高为10,抽查结果统计如下:
(1)成下列频率分布直方图;
(2)估计这20名用户满意度的中位数;
(3)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,现从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.
| 满意度分组 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
| 用户数 | 1 | 2 | 4 | 5 | 8 |

(2)估计这20名用户满意度的中位数;
(3)设第四组(即满意度在区间[6,8)内)的5名用户的满意度数据分别为:6.5,7,7.5,7.5,7.9,现从中任取两名不同用户的满意度数据x、y,求|x-y|<1的概率.