题目内容
甲、乙两人用两颗骰子做游戏,规则如下:若某人掷出的两颗骰子向上的点数之和为3的倍数,则该人继续投掷;若投出的点数之和不是3的倍数,则由对方接着投掷.第一次由甲开始投掷.(1)设第n次是由甲投掷的概率为Pn,求Pn;
(2)前三次投掷中,恰好甲投掷两次的概率是多少?
答案:(1)两颗骰子向上的点数之和为3的倍数的情况有1+2,1+5,2+1,2+4,3+3,3+6,4+2,4+5,5+1,5+4,6+3,6+6共12种.所以投掷一次向上点数之和为3的倍数的概率是![]() .
.
又“第n次由甲投掷”这一事件包括“第n-1次由甲投掷,第n次仍由甲投掷”和“第n-1次由乙投掷,第n次由甲投掷”两种情形,
∴Pn=![]() Pn-1+(1
Pn-1+(1![]() )(1-Pn-1)=
)(1-Pn-1)=![]() Pn-1
Pn-1![]() Pn
Pn![]() (Pn-1
(Pn-1![]() ).
).
于是{Pn![]() }是公比为
}是公比为![]() 的等比数列,从而Pn
的等比数列,从而Pn![]() =(P1
=(P1![]() )·(
)·(![]() )n-1.
)n-1.
∵P1=1,∴Pn![]() .
.
故Pn=![]() [1+(
[1+(![]() )n-1].
)n-1].
(2)由(1)知,P1=1,P2=![]() ,P3=
,P3=![]() ,
,
由于规定第一次是甲投掷,所以前三次投掷中甲恰好投掷两次的情形只有两种:
甲甲乙,甲乙甲,因而其概率为
P=1×![]() .
.

练习册系列答案
相关题目
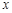 ,第二次出现的点数为
,第二次出现的点数为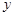 ,用
,用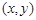 表示先后抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
表示先后抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果. ,第二次出现的点数为
,第二次出现的点数为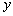 ,用
,用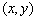 表示先后抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
表示先后抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.