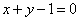Question

（1）求直线2x+11y+16=0关于点P（0，1）对称的直线方程．
（2）求直线2x-y+1=0关于直线x-y+2=0对称的直线方程．
（3）两平行直线3x+4y-1=0与6x+8y+3=0关于直线l对称，求l的方程．

Answer 1

分析：（1）由题意，得所求直线与直线2x+11y+16=0平行且P点到两直线的距离相等．因此设所求直线方程为2x+11y+C=0，利用点到直线的距离列式，解出C值即可得到所求对称直线方程；
（2）根据题意，设所求直线上任一点M（x，y）且M关于直线x-y+2=0的对称点M'（x₁，y₁），利用轴对称的性质列出方程组解出用x、y表示x₁、y₁的式子，再由点M'在直线2x-y+1=0上代入，化简即得所求对称直线方程；
（3）根据题意，直线l与3x+4y-1=0、6x+8y+3=0平行，且l到两直线的距离相等，再利用点到直线的距离公式列式，即可解出直线l的方程．

解答：解：（1）∵所求直线与直线2x+11y+16=0关于点P（0，1）对称
∴所求直线与直线2x+11y+16=0平行，它们到P点距离相等，
因此，设所求直线方程为2x+11y+C=0，可得

|2×0+11×1+16|

22+112

=

|2×0+11×1+C|

22+112

，解之得C=-38（舍去16），
∴所求直线2x+11y-38=0．
（2）设所求直线上任一点M（x，y），M关于直线x-y+2=0的对称点M'（x₁，y₁），
则

y-y1 x-x1 =-1 2• x+x1 2 - y+y1 2 +2=0

，解出

x1=y-2 y1=x+2

（*）
∵点M'在直线2x-y+1=0上，满足2x₁-y₁+1=0
∴将（*）式代入，得2（y-2）-（x+2）+1=0，
化简得x-2y+5=0，即为直线2x-y+1=0关于直线x-y+2=0对称的直线方程．
（3）∵两平行直线3x+4y-1=0与6x+8y+3=0关于直线l对称，
∴直线l是与两直线平行且距离相等且与它们平行的一条直线，
设l：6x+8y+C=0，可得

|C-3|

62+82

=

|C+2|

62+82

，解之得C=

1

2

，
即直线3x+4y-1=0与6x+8y+3=0的对称轴l方程为：6x+8y+

1

2

=0．

点评：本题要我们求直线关于点的对称直线、直线关于直线的对称直线和两条平行线构成图形的对称轴．着重考查了直线的基本量与基本形式、点到直线的距离公式和轴对称的性质等知识，属于中档题．