题目内容
分别以双曲线 的实轴、虚轴为椭圆的长轴、短轴,求该椭圆的方程.
的实轴、虚轴为椭圆的长轴、短轴,求该椭圆的方程.
【答案】分析:先确定双曲线 的实轴长、虚轴长,进而可得椭圆的长轴长、短轴长,焦点在x轴上,从而可求椭圆的标准方程.
的实轴长、虚轴长,进而可得椭圆的长轴长、短轴长,焦点在x轴上,从而可求椭圆的标准方程.
解答:解:∵双曲线
∴双曲线的焦点在x轴上,且a=5,b=4
∵双曲线 的实轴、虚轴为椭圆的长轴、短轴
的实轴、虚轴为椭圆的长轴、短轴
∴椭圆的长轴长、短轴长分别为10,8,焦点在x轴上,
∴椭圆的标准方程为:
点评:本题重点考查椭圆的几何性质,考查椭圆的标准方程,确定双曲线 的实轴长、虚轴长是关键.
的实轴长、虚轴长是关键.
 的实轴长、虚轴长,进而可得椭圆的长轴长、短轴长,焦点在x轴上,从而可求椭圆的标准方程.
的实轴长、虚轴长,进而可得椭圆的长轴长、短轴长,焦点在x轴上,从而可求椭圆的标准方程.解答:解:∵双曲线

∴双曲线的焦点在x轴上,且a=5,b=4
∵双曲线
 的实轴、虚轴为椭圆的长轴、短轴
的实轴、虚轴为椭圆的长轴、短轴∴椭圆的长轴长、短轴长分别为10,8,焦点在x轴上,
∴椭圆的标准方程为:

点评:本题重点考查椭圆的几何性质,考查椭圆的标准方程,确定双曲线
 的实轴长、虚轴长是关键.
的实轴长、虚轴长是关键. 
练习册系列答案
相关题目
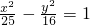 的实轴、虚轴为椭圆的长轴、短轴,求该椭圆的方程.
的实轴、虚轴为椭圆的长轴、短轴,求该椭圆的方程.