题目内容
已知二次函数f(x)=ax2+bx+c的图象过A(t1,y1)、B(t2,y2)两点,且满足a2+(y1+y2)a+y1y2=0.(1)证明y1=-a或y2=-a;
(2)证明函数f(x)的图象必与x轴有两个交点;
(3)若关于x的不等式f(x)>0的解集为{x|x>m或x<n,n<m<0},解关于x的不等式cx2-bx+a>0.
【答案】分析:(1)由题知a2+(y1+y2)a+y1y2=0解得y1或y2即可;
(2)讨论a>0,函数为开口向上的抛物线,a<0时函数图象开口向下,由(2)得图象上的点A、B的纵坐标大于小于0得到与x轴有两个交点即可;
(3)根据已知不等式的解集得到a的符号且可得ax2+bx+c=0的两根为m,n,然后利用根与系数的关系化简不等式求出解集即可.
解答:解:(1)证明:∵a2+(y1+y2)a+y1y2=0,
∴(a+y1)(a+y2)=0,得y1=-a或y2=-a.
(2)证明:当a>0时,二次函数f(x)的图象开口向上,图象上的点A、B的纵坐标至少有一个为-a且小于零,
∴图象与x轴有两个交点.
当a<0时,二次函数f(x)的图象开口向下,图象上的点A、B的纵坐标至少有一个为-a且大于零,
∴图象与x轴有两个交点.
故二次函数f(x)的图象与x轴有两个不同的交点.
(3)∵ax2+bx+c>0的解集为{x|x>m或x<n,n<m<0}.
根据一元二次不等式大于0取两边,从而可判定a>0,
并且可得ax2+bx+c=0的两根为m,n,
∴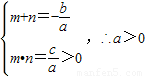
∴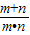 =
=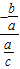 =-
=-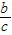 .
.
而cx2-bx+a>0?x2-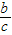 x+
x+ >0?x2+(
>0?x2+(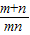 )x+
)x+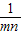 >0?(x+
>0?(x+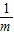 )(x+
)(x+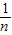 )>0,
)>0,
又∵n<m<0,∴-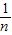 <-
<-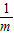 ,∴x>-
,∴x>-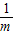 或x<-
或x<-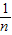 .
.
故不等式cx2-bx+a>0的解集为{x|x>-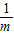 或x<-
或x<-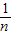 }.
}.
点评:考查学生函数与方程的综合运用能力,以及一元二次方程根与系数关系的灵活运用,不等式取解集方法的运用能力.
(2)讨论a>0,函数为开口向上的抛物线,a<0时函数图象开口向下,由(2)得图象上的点A、B的纵坐标大于小于0得到与x轴有两个交点即可;
(3)根据已知不等式的解集得到a的符号且可得ax2+bx+c=0的两根为m,n,然后利用根与系数的关系化简不等式求出解集即可.
解答:解:(1)证明:∵a2+(y1+y2)a+y1y2=0,
∴(a+y1)(a+y2)=0,得y1=-a或y2=-a.
(2)证明:当a>0时,二次函数f(x)的图象开口向上,图象上的点A、B的纵坐标至少有一个为-a且小于零,
∴图象与x轴有两个交点.
当a<0时,二次函数f(x)的图象开口向下,图象上的点A、B的纵坐标至少有一个为-a且大于零,
∴图象与x轴有两个交点.
故二次函数f(x)的图象与x轴有两个不同的交点.
(3)∵ax2+bx+c>0的解集为{x|x>m或x<n,n<m<0}.
根据一元二次不等式大于0取两边,从而可判定a>0,
并且可得ax2+bx+c=0的两根为m,n,
∴
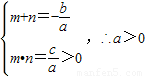
∴
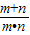 =
=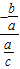 =-
=-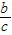 .
.而cx2-bx+a>0?x2-
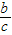 x+
x+ >0?x2+(
>0?x2+(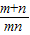 )x+
)x+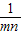 >0?(x+
>0?(x+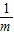 )(x+
)(x+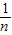 )>0,
)>0,又∵n<m<0,∴-
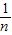 <-
<-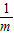 ,∴x>-
,∴x>-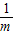 或x<-
或x<-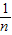 .
.故不等式cx2-bx+a>0的解集为{x|x>-
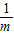 或x<-
或x<-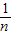 }.
}.点评:考查学生函数与方程的综合运用能力,以及一元二次方程根与系数关系的灵活运用,不等式取解集方法的运用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目