题目内容
已知命题p:x2-3x-4≤0;q:(x-1)2-a2≥0(a>0).若p是?q的充分不必要条件,求a的取值范围.
分析:通过解不等式求得命题P、q为真时a的范围,再根据p是?q的充分不必要条件分析求解.
解答:解:由x2-3x-4≤0⇒-1≤x≤4,
由(x-1)2-a2≥0⇒(x-1+a)(x-1-a)≥0⇒x≥1+a或x≤1-a
∵p是?q的充分不必要条件⇒q是¬P的充分不必要条件
∵¬P是 x>4或x<-1
∴
⇒a>3
综上a的取值范围是a>3
由(x-1)2-a2≥0⇒(x-1+a)(x-1-a)≥0⇒x≥1+a或x≤1-a
∵p是?q的充分不必要条件⇒q是¬P的充分不必要条件
∵¬P是 x>4或x<-1
∴
|
综上a的取值范围是a>3
点评:本题借助考查充分不必要条件的判断及应用,考查命题的否定及命题与其逆否命题的同真性.
若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件.
若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
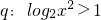 ,则命题p是q的
,则命题p是q的 ,则命题p是q的( )
,则命题p是q的( )