题目内容
已知函数f(x)=plnx+(p-1)x2+1。
(1) 当p=1时,f(x)≤λx恒成立,求实数λ的取值范围。
(2) 当p>0时,讨论函数f(x)的单调性。
(1) 当p=1时,f(x)≤λx恒成立,求实数λ的取值范围。
(2) 当p>0时,讨论函数f(x)的单调性。
解:(1)当p=1时,f(x)≤kx恒成立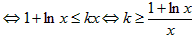 ,f(x)的定义域为(0,+∞)令
,f(x)的定义域为(0,+∞)令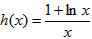 ,则
,则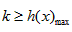 ,
,
因为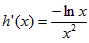 ,由
,由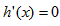 ,得x=1,
,得x=1,
且当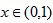 时,
时,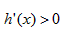 ;当
;当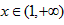 时,
时,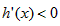 ,
,
所以h(x)在(0,1)上递增,在(1,+∞)上递减,所以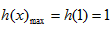 ,
,
故k≥1;
(2)f(x)的定义域为(0,+∞),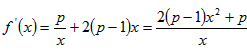 …
…
当p>1时,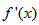 >0,故f(x)在(0,+∞)单调递增;
>0,故f(x)在(0,+∞)单调递增;
当0<p<1时,令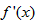 =0,解得
=0,解得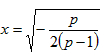 ,
,
则当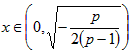 时,f′(x)>0;
时,f′(x)>0;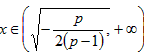 时,
时,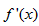 <0,
<0,
故f(x)在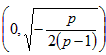 单调递增,在
单调递增,在 单调递减。
单调递减。
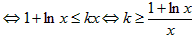 ,f(x)的定义域为(0,+∞)令
,f(x)的定义域为(0,+∞)令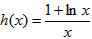 ,则
,则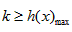 ,
, 因为
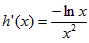 ,由
,由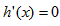 ,得x=1,
,得x=1,且当
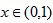 时,
时,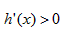 ;当
;当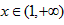 时,
时,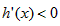 ,
,所以h(x)在(0,1)上递增,在(1,+∞)上递减,所以
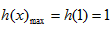 ,
,故k≥1;
(2)f(x)的定义域为(0,+∞),
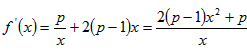 …
…当p>1时,
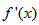 >0,故f(x)在(0,+∞)单调递增;
>0,故f(x)在(0,+∞)单调递增;当0<p<1时,令
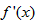 =0,解得
=0,解得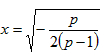 ,
,则当
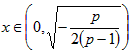 时,f′(x)>0;
时,f′(x)>0;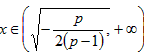 时,
时,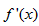 <0,
<0,故f(x)在
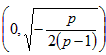 单调递增,在
单调递增,在 单调递减。
单调递减。 
练习册系列答案
相关题目