题目内容
已知函数f(x)=ax2+4(a为非零实数),设函数F(x)=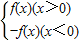 .
.(1)若f(-2)=0,求F(x)的表达式;
(2)设mn<0,m+n>0,试判断F(m)+F(n)能否大于0?
【答案】分析:(1)由-2<0,故应代入f(x)=-ax2-4式求参数的值.
(2)确定m,n的符号代入相应的解析式依据其形式进行判断.因为 m,n的符号有两个组合,又两种情况下解题结论是一样的,故只证其一种,
解答:解:(1)由f(-2)=0,4a+4=0⇒a=-1,
∴F(x)=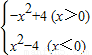 .
.
(2)∵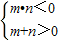 ,∴m,n一正一负.
,∴m,n一正一负.
不妨设m>0且n<0,则m>-n>0,m2>n2
F(m)+F(n)=f(m)-f(n)=am2+4-(an2+4)
=a(m2-n2),
当a>0时,F(m)+F(n)能大于0,
当a<0时,F(m)+F(n)不能大于0.
综上,当a>0时,F(m)+F(n)能大于0,
点评:本题考点是分段函数,考查了求分段函数的解析式,以及根据分段函数的定义选择解析式判断符号.
(2)确定m,n的符号代入相应的解析式依据其形式进行判断.因为 m,n的符号有两个组合,又两种情况下解题结论是一样的,故只证其一种,
解答:解:(1)由f(-2)=0,4a+4=0⇒a=-1,
∴F(x)=
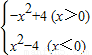 .
.(2)∵
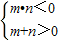 ,∴m,n一正一负.
,∴m,n一正一负.不妨设m>0且n<0,则m>-n>0,m2>n2
F(m)+F(n)=f(m)-f(n)=am2+4-(an2+4)
=a(m2-n2),
当a>0时,F(m)+F(n)能大于0,
当a<0时,F(m)+F(n)不能大于0.
综上,当a>0时,F(m)+F(n)能大于0,
点评:本题考点是分段函数,考查了求分段函数的解析式,以及根据分段函数的定义选择解析式判断符号.

练习册系列答案
相关题目