题目内容
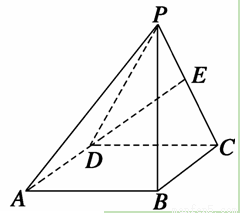
如图，四棱锥P－ABCD中，底面四边形ABCD是正方形，侧面PDC是边长为a的正三角形，且平面PDC⊥平面ABCD，E为PC的中点．
(1)求异面直线PA与DE所成的角的余弦值．
(2)求点D到平面PAB的距离．
【答案】
解 如图取DC的中点O，连结PO，
∵△PDC为正三角形，∴PO⊥DC
又∵面PDC⊥面ABCD
∴PO⊥面ABCD
∴以O为坐标原点OC、OP所在直线为y轴，z轴建立如图所示直角坐标系，
则P(0,0，
a)，A(a，
,0)，B(a，
,0)，C(0，,0)，
D(0，,0)．
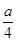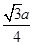(1)∵E为PC的中点，∴E(0，
，
)
＝(0，a,0)，
＝(0，a,0)，
设平面PAB的一个法向量为n＝(x，y，z)，则
n⊥
，n⊥＝(0，a,0)，
【解析】略
练习册系列答案
名校课堂系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，CE∥AB．
如图，四棱锥P-ABCD的底面ABCD是正方形，AC∩BD=O，PA⊥底面ABCD，OE⊥PC于E．
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥平面ABCD，点E，F分别是AB和PC的中点．
如图，四棱锥P-ABCD，PA⊥底面ABCD，AB∥CD，AB⊥AD，AB=AD=