题目内容
下列说法错误 的是( )
分析:由复合命题真假判断的真值表,我们可以判断出A的真假,由特称命题的否定方法,我们可以写出原命题的否定,进而判断出B的真假;由四种命题的定义,我们可以求出原命题的否命题,进而得到C的真假;根据一元二次方程根的个数与△的关系,我们可以判断出D的真假,进而得到答案.
解答:解:如果命题“?p”是真命题,则命题p为假命题,
又由命题“p或q”是真命题,故命题q一定是真命题,故A正确;
命题p:?x0∈R,x02-2x0+4<0,的否定为:?x∈R,x2-2x+4≥0,故B正确;
命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”故C正确;
方程-2x2+x-4=0的△=1-32<0,故方程-2x2+x-4=0无实根
故特称命题“?x∈R,使-2x2+x-4=0”是假命题,故D错误
故选D
又由命题“p或q”是真命题,故命题q一定是真命题,故A正确;
命题p:?x0∈R,x02-2x0+4<0,的否定为:?x∈R,x2-2x+4≥0,故B正确;
命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”故C正确;
方程-2x2+x-4=0的△=1-32<0,故方程-2x2+x-4=0无实根
故特称命题“?x∈R,使-2x2+x-4=0”是假命题,故D错误
故选D
点评:本题考查的知识点是命题的真假判断,复合命题的真假判断,特称命题的否定,四种命题,方程根的存在判断,其中根据上述知识点判断各命题的真假是解答本题的关键.

练习册系列答案
相关题目
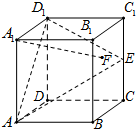 在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法错误的是( )
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,记A1F与平面BCC1B1所成的角为θ,下列说法错误的是( )| A、点F的轨迹是一条线段 | ||
| B、A1F与D1E不可能平行 | ||
| C、A1F与BE是异面直线 | ||
D、tanθ≤2
|
 如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )
如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )