题目内容
(2007
北京崇文模拟)如图所示,已知双曲线C的中心点为坐标原点O,焦点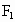 、
、 在x轴上,点P在双曲线的左支上,点M在右准线上,且满足
在x轴上,点P在双曲线的左支上,点M在右准线上,且满足 ,
, .
.
(1)
求双曲线C的离心率e;(2)
若双曲线C过点Q(2, ),
), 、
、 是双曲线虚轴的上、下端点,点A、B是双曲线上不同的两点,且
是双曲线虚轴的上、下端点,点A、B是双曲线上不同的两点,且 ,
, ,求直线AB的方程.
,求直线AB的方程.

答案:略
解析:
解析:
|
解析: (1)设双曲线C的方程为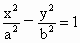 (a>0,b>0), (a>0,b>0),
且 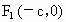 , ,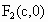 . .
∵ 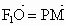 , ,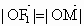 , ,
∴四边形 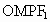 为菱形. 为菱形.
∴ 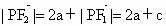 , ,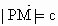 . .
∴ 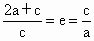 ,∴e=2. ,∴e=2.
(2) 由(1)知e=2,∴c=2a,∴ 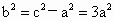 , ,
∴双曲线 C的方程为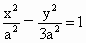 , ,
双曲线 C过点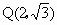 , ,
∴ 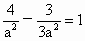 , , , ,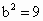 . .
∴双曲线 C的方程为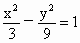 . .
∵ 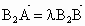 ,∴A、 ,∴A、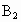 、B三点共线. 、B三点共线.
∵ 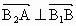 ,∴ ,∴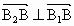 . .
(i) 当直线AB垂直x轴时,不合题意.(ii) 当直线AB不垂直x轴时,由 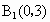 , ,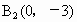 , ,
可设直线 AB的方程为y=kx-3, ①∴直线 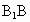 的方程为 的方程为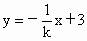 . ② . ②
由①②知 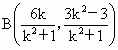 ,代入双曲线方程得 ,代入双曲线方程得
∴ 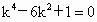 ,解得 ,解得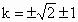 , ,
故直线 AB的方程为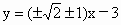 . . |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
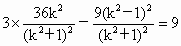
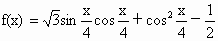 .
.
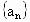 中,对任意
中,对任意 ,都有
,都有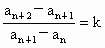 (k为常数),则称
(k为常数),则称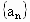 为“等差比数列”,下面对“等差比数列”的判断:①k不可能为0;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④通项公式为
为“等差比数列”,下面对“等差比数列”的判断:①k不可能为0;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④通项公式为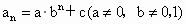 的数列一定是等差比数列,其中正确的判断
的数列一定是等差比数列,其中正确的判断
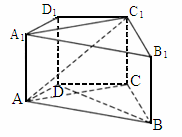
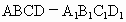 中,M是
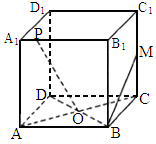
中,M是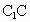 的中点,O是底面ABCD的中心,P是
的中点,O是底面ABCD的中心,P是 上的任意点,则直线BM与OP所成的角为__________°.
上的任意点,则直线BM与OP所成的角为__________°.
 中,∠ADC=90°,△ABC为等边三角形,且
中,∠ADC=90°,△ABC为等边三角形,且 .
.
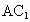 与BC所成角的余弦值;
与BC所成角的余弦值;
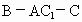 的大小;
的大小;
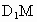 ⊥平面
⊥平面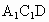 ?并证明你的结论.
?并证明你的结论.
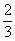 和
和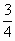 ,假设两人每次射击是否击中目标相互之间没有影响.
,假设两人每次射击是否击中目标相互之间没有影响.