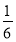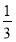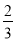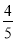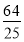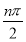题目内容
如图，点P(0，－1)是椭圆C1：
＝1(a>b>0)的一个顶点，C1的长轴是圆C2：x2＋y2＝4的直径．l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A，B两点，l2交椭圆C1于另一点D.
(1)求椭圆C1的方程；
(2)求当△ABD的面积取最大值时，直线l1的方程．
（1）
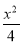＋y2＝1.（2）y＝±
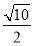x－1
【解析】(1)由题意得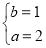
，所以椭圆C的方程为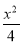＋y2＝1.
(2)设A(x1，y1)，B(x2，y2)，D(x0，y0)．
由题意知直线l1的斜率存在，不妨设其为k，
则直线l1的方程为y＝kx－1.又圆C2：x2＋y2＝4，
故点O到直线l1的距离d＝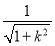
，
所以|AB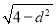|＝2
＝2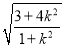
.
又l2⊥l1，故直线l2的方程为x＋ky＋k＝0.由
消去y，整理得(4＋k2)x2＋8kx＝0，故x0＝－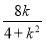
.所以|PD|＝
.
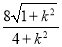设△ABD的面积为S，则S＝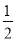
·|AB|·|PD|＝
，
所以S＝
≤
＝
，
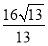当且仅当k＝±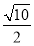
时取等号．
所以所求直线l1的方程为y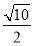＝±x－1.
练习册系列答案
相关题目
