题目内容
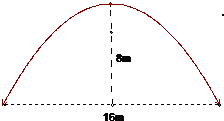 如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.
如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.(1)一条船船顶部宽4m,要使这艘船安全通过,则 船在水面以上部分高不能超过多少米?
(2)近日因受台风影响水位暴涨2.7m,为此必须加重船载,降低船身,才能通过桥洞.试问:一艘顶部宽4
| 2 |
分析:(1)设抛物线方程x2=-2py,抛物线过点点(8,-8)代入抛物线方程求出参数p 即得抛物线方程,最后令其x=2即可得出船在水面以上部分高不能超过多少米.
(2)把x=2
代入抛物线的方程求得y值,由1+0.5+2.7+4=8.2,可知船身应至少降低0.2米能安全通过此桥.
(2)把x=2
| 2 |
解答: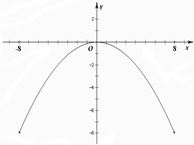 解:(1)如图所示,以过拱桥的最高点且平行水面的直线为X轴,最高点O为原点建立直角坐标系(1分)
解:(1)如图所示,以过拱桥的最高点且平行水面的直线为X轴,最高点O为原点建立直角坐标系(1分)
设抛物线方程为x2=-2py,将点(8,-8)代入得2p=8,
∴抛物线方程是x2=-8y,(4分)
将x=2代入得y=-
,8-0.5-0.5=7,
故船在水面以上部分高不能超过7米.(6分)
(2)将x=2
代入方程x2=-8y得y=-1,(8分)
此时1+0.5+2.7+4=8.2,
故船身应至少降低0.2米(10分)
 解:(1)如图所示,以过拱桥的最高点且平行水面的直线为X轴,最高点O为原点建立直角坐标系(1分)
解:(1)如图所示,以过拱桥的最高点且平行水面的直线为X轴,最高点O为原点建立直角坐标系(1分)设抛物线方程为x2=-2py,将点(8,-8)代入得2p=8,
∴抛物线方程是x2=-8y,(4分)
将x=2代入得y=-
| 1 |
| 2 |
故船在水面以上部分高不能超过7米.(6分)
(2)将x=2
| 2 |
此时1+0.5+2.7+4=8.2,
故船身应至少降低0.2米(10分)
点评:本题考查用待定系数法求抛物线的标准方程的方法,以及利用抛物线的方程解决实际问题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
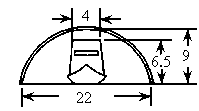
 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
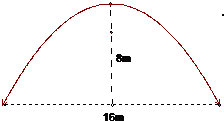 如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.
如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m. m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?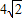 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?