题目内容
在平面几何里,已知直角三角形ABC中,角C为90°,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
有三角形的勾股定理,给出空间中三棱锥的有关结论:
若三角形ABC的外接圆的半径为r=
,给出空间中三棱锥的有关结论:
有三角形的勾股定理,给出空间中三棱锥的有关结论:
在三棱锥O-ABC中,若三个侧面两两垂直,则
+
+
=
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
在三棱锥O-ABC中,若三个侧面两两垂直,则
+
+
=
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
若三角形ABC的外接圆的半径为r=
| ||
| 2 |
在三棱锥O-ABC中,若三个侧面两两垂直,且三条侧棱长分别为a,b,c,则其外接球的半径为r=
| ||
| 2 |
在三棱锥O-ABC中,若三个侧面两两垂直,且三条侧棱长分别为a,b,c,则其外接球的半径为r=
.
| ||
| 2 |
分析:(1)这是一个类比推理的题,斜边的平方等于两个直角边的平方和,可类比到空间就是斜面面积的平方等于三个直角面的面积的平方和,边对应着面.
(2)在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知在平面几何中在△ABC中,若∠C=90°,AC=b,BC=a,则△ABC的外接圆的半径r=
,我们可以类比这一性质,推理出在空间中有三条侧棱两两垂直的四面体O-ABC中类似的结论.
(2)在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知在平面几何中在△ABC中,若∠C=90°,AC=b,BC=a,则△ABC的外接圆的半径r=
| ||
| 2 |
解答:解:(1)由边对应着面,边长对应着面积,
由类比可得:在三棱锥O-ABC中,若三个侧面两两垂直,则
+
+
=
(2)由平面图形的性质类比推理空间图形的性质时,
一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由圆的性质推理到球的性质.
由已知在平面几何中,△ABC中,若∠C=90°,AC=b,BC=a,则△ABC的外接圆的半径r=
,
我们可以类比这一性质,推理出:在三棱锥O-ABC中,若三个侧面两两垂直,且三条侧棱长分别为a,b,c,则其外接球的半径为r=
,
故答案为:在三棱锥O-ABC中,若三个侧面两两垂直,则
+
+
=
;
在三棱锥O-ABC中,若三个侧面两两垂直,且三条侧棱长分别为a,b,c,则其外接球的半径为r=
.
由类比可得:在三棱锥O-ABC中,若三个侧面两两垂直,则
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
(2)由平面图形的性质类比推理空间图形的性质时,
一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由圆的性质推理到球的性质.
由已知在平面几何中,△ABC中,若∠C=90°,AC=b,BC=a,则△ABC的外接圆的半径r=
| ||
| 2 |
我们可以类比这一性质,推理出:在三棱锥O-ABC中,若三个侧面两两垂直,且三条侧棱长分别为a,b,c,则其外接球的半径为r=
| ||
| 2 |
故答案为:在三棱锥O-ABC中,若三个侧面两两垂直,则
| S | 2 △OAB |
| S | 2 △OAC |
| S | 2 △OBC |
| S | 2 △ABC |
在三棱锥O-ABC中,若三个侧面两两垂直,且三条侧棱长分别为a,b,c,则其外接球的半径为r=
| ||
| 2 |
点评:本题主要考查学生知识的迁移类比等基本能力,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
相关题目
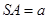 ,
,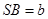 则
则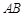 边上的高
边上的高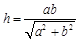 ; 拓展到空间,如图,三棱锥
; 拓展到空间,如图,三棱锥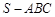 的三条侧棱SB、SB、SC两两相互垂直,且
的三条侧棱SB、SB、SC两两相互垂直,且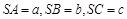 ,则点
,则点 到面
到面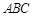 的距离
的距离
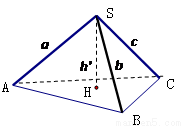

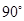 ,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论: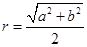 ,给出空间中三棱锥的有关结论:________
,给出空间中三棱锥的有关结论:________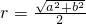 ,给出空间中三棱锥的有关结论:________.
,给出空间中三棱锥的有关结论:________.