题目内容
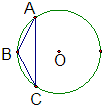（几何证明选讲选做题）如图所示，等腰三角形ABC的底边AC长为8，其外接圆的半径长为5，则三角形ABC的面积是分析：根据等腰三角形ABC的底边AC长为8，其外接圆的半径长为5，由勾股定理可知弦心距，对于三角形已知高和对应的边长，求出面积．
解答：解：∵等腰三角形ABC的底边AC长为8，其外接圆的半径长为5
∴半径，弦心距和弦长组成一个直角三角形，有勾股定理可知弦心距是
=3，
∴三角形的高是5-3=2，
∴三角形的面积是
×2×8=8，
故答案为：8
∴半径，弦心距和弦长组成一个直角三角形，有勾股定理可知弦心距是
| 25-16 |
∴三角形的高是5-3=2，
∴三角形的面积是
| 1 |
| 2 |
故答案为：8
点评：本题考查三角形的面积公式，是一个基础题，解题的关键是构造直角三角形，在圆中这个直角三角形是经常用来求解线段的长度的．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
（几何证明选讲选做题）
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（几何证明选讲选做题）
（几何证明选讲选做题）