题目内容
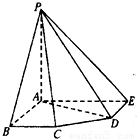
如图，在五棱锥P－ABCDE中，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC．∠ABC＝45°，AB＝2
，BC＝2AE＝4，三角形PAB是等腰三角形．
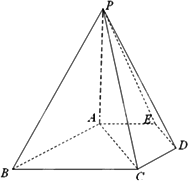
(Ⅰ)求证：平面PCD⊥平面PAC；
(Ⅱ)求二面角P―ED―B的正切值；
(Ⅲ)求直线PB与平面PCD所成角的大小．
答案：
解析：
解析：
|
(Ⅰ)证明：因为 所以在 所以 又PA⊥平面ABCDE，所以PA⊥ 又PA 又AB∥CD，所以 又因为 (Ⅱ)由过 由PA⊥平面ABCDE，由三垂线定理可知 则 因为三角形 又可求得 所以二面角 |
ABC＝45°，AB＝2
，BC＝4，
中，由余弦定理得：
，解得
，
，即
，
，所以
，
，
，所以平面PCD⊥平面PAC 4分
作
于
，连接
是二面角
的平面角，
是等腰三角形，所以
，
，所以
，
练习册系列答案
相关题目
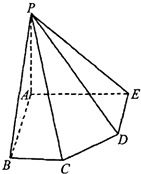
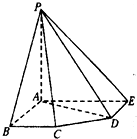如图，在五棱锥P-ABCDE中，PA=AB=AE=2a，PB=PE=
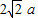，BC=DE=a，∠EAB=∠ABC=∠DEA=90°．
