题目内容
已知n∈N*,设函数fn(x)=1-x+
-
+…-
,x∈R.
(1)求函数y=f2(x)-kx(k∈R)的单调区间;
(2)是否存在整数t,对于任意n∈N*,关于x的方程fn(x)=0在区间[t,t+1]上有唯一实数解?若存在,求t的值;若不存在,说明理由.
| x2 |
| 2 |
| x3 |
| 3 |
| x2n-1 |
| 2n-1 |
(1)求函数y=f2(x)-kx(k∈R)的单调区间;
(2)是否存在整数t,对于任意n∈N*,关于x的方程fn(x)=0在区间[t,t+1]上有唯一实数解?若存在,求t的值;若不存在,说明理由.
(1)因为y=f2(x)-kx=1-x+
-
-kx,
所以y′=-1+x-x2-k=-(x2-x+k+1),
方程x2-x+k+1=0的判别式△=(-1)2-4(k+1)=-3-4k,
当k≥-
时,△≤0,y′=-(x2-x+k+1)≤0,
故函数y=f2(x)-kx在R上单调递减;
当k<-
时,方程x2-x+k+1=0的两根为x1=
,x2=
,
则x∈(-∞,x1)时,y′<0,x∈(x1,x2)时,y′>0,x∈(x2,+∞)时,y′<0,
故函数y=f2(x)-kx(k∈R)的单调递减区间为(-∞,x1)和(x2,+∞),单调递增区间为(x1,x2);
(2)存在t=1,对于任意n∈N*,关于x的方程fn(x)=0在区间[t,t+1]上有唯一实数解,理由如下:
当n=1时,f1(x)=1-x,令f1(x)=1-x=0,解得x=1,
所以关于x的方程f1(x)=0有唯一实数解x=1;
当n≥2时,由fn(x)=1-x+
-
+…-
,
得fn′(x)=-1+x-x2+…+x2n-3-x2n-2,
若x=-1,则f′n(x)=f′n(-1)=-(2n-1)<0,
若x=0,则f′n(x)=-1<0,
若x≠-1且x≠0时,则f′n(x)=-
,
当x<-1时,x+1<0,x2n-1+1<0,f′n(x)<0,
当x>-1时,x+1>0,x2n-1+1>0,f′n(x)<0,
所以f′n(x)<0,故fn(x)在(-∞,+∞)上单调递减.
因为fn(1)=(1-1)+(
-
)+(
-
)+…+(
-
)>0,
fn(2)=(1-2)+(
-
)+(
-
)+…+(
-
)
=-1+(
-
)•22+(
-
)•24+…+(
-
)•22n-2
=-1-
•22-
•24-…-
•22n-2<0,
所以方程fn(x)=0在[1,2]上有唯一实数解,
综上所述,对于任意n∈N*,关于x的方程fn(x)=0在区间[1,2]上有唯一实数解,所以t=1.
| x2 |
| 2 |
| x3 |
| 3 |
所以y′=-1+x-x2-k=-(x2-x+k+1),
方程x2-x+k+1=0的判别式△=(-1)2-4(k+1)=-3-4k,
当k≥-
| 3 |
| 4 |
故函数y=f2(x)-kx在R上单调递减;
当k<-
| 3 |
| 4 |
1-
| ||
| 2 |
1+
| ||
| 2 |
则x∈(-∞,x1)时,y′<0,x∈(x1,x2)时,y′>0,x∈(x2,+∞)时,y′<0,
故函数y=f2(x)-kx(k∈R)的单调递减区间为(-∞,x1)和(x2,+∞),单调递增区间为(x1,x2);
(2)存在t=1,对于任意n∈N*,关于x的方程fn(x)=0在区间[t,t+1]上有唯一实数解,理由如下:
当n=1时,f1(x)=1-x,令f1(x)=1-x=0,解得x=1,
所以关于x的方程f1(x)=0有唯一实数解x=1;
当n≥2时,由fn(x)=1-x+
| x2 |
| 2 |
| x3 |
| 3 |
| x2n-1 |
| 2n-1 |
得fn′(x)=-1+x-x2+…+x2n-3-x2n-2,
若x=-1,则f′n(x)=f′n(-1)=-(2n-1)<0,
若x=0,则f′n(x)=-1<0,
若x≠-1且x≠0时,则f′n(x)=-
| x2n-1+1 |
| x+1 |
当x<-1时,x+1<0,x2n-1+1<0,f′n(x)<0,
当x>-1时,x+1>0,x2n-1+1>0,f′n(x)<0,
所以f′n(x)<0,故fn(x)在(-∞,+∞)上单调递减.
因为fn(1)=(1-1)+(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2n-2 |
| 1 |
| 2n-1 |
fn(2)=(1-2)+(
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| 4 |
| 25 |
| 5 |
| 22n-2 |
| 2n-2 |
| 22n-1 |
| 2n-1 |
=-1+(
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 5 |
| 1 |
| 2n-2 |
| 2 |
| 2n-1 |
=-1-
| 1 |
| 2•3 |
| 3 |
| 4•5 |
| 2n-3 |
| (2n-2)(2n-1) |
所以方程fn(x)=0在[1,2]上有唯一实数解,
综上所述,对于任意n∈N*,关于x的方程fn(x)=0在区间[1,2]上有唯一实数解,所以t=1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 对一切n∈N*均成立的最大实数a;
对一切n∈N*均成立的最大实数a;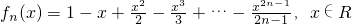 .
.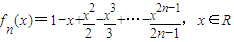 .
.