题目内容
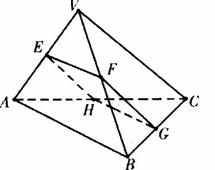
正三棱锥V-ABC的底面边长为2a，E、F、G、H分别是VA、VB、BC、AC的中点，则四边形EFGH面积的取值范围是 ( )A.(0，+∞) B.(
，+∞) C.(
，+∞) D.(
，+∞)
答案：B 【解析】本题考查空间位置关系的推证及运算.据题意易知四边形EFGH平行四边形,又由于三棱锥为正三棱锥故VC⊥AB,又EH∥VC,HG∥AB,故EH⊥HG,即平行四边形为矩形,又设三棱锥侧棱长为l,由其侧面展开图为三个全等的等腰三角形,易知若三个三角形能折叠为三棱锥的侧面,则需每个三角形的顶角小于120°,即cos∠AVB=＞cos120°l＞
a,故S矩形EFCH=|EH|·|HG|＞
a×a=
a2.
练习册系列答案
名校课堂系列答案
相关题目
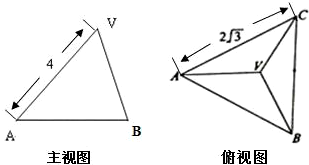已知正三棱锥V-ABC的主视图，俯视图如图所示，其中VA=4，AC=2| 3 |
| A、9 | ||
| B、6 | ||
C、3
| ||
D、
|
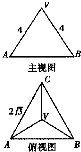如图是正三棱锥V-ABC的主视图，俯视图，根据图中尺寸，则该三棱锥的侧视图面积为（ ）| A、9 | ||||
| B、6 | ||||
C、
| ||||
D、
|
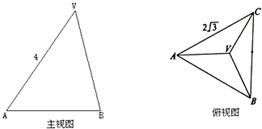（2010•汕头模拟）已知正三棱锥V-ABC的主视图、俯视图如下图所示，其中