题目内容
如图,正△ABC的边长为3,过其中心G作BC边的平行线,分别交AB、AC于B1、C1,将△AB1C1沿B1C1折起到△A1B1C1的位置,使点A1在平面BB1C1C上的射影恰是线段BC的中点M,求: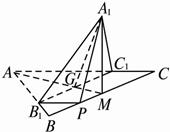
(1)二面角A1B1C1M的大小;
(2)异面直线A1B1与CC1所成角的大小(用反三角函数表示).
解析:(1)连结AM、A1G,∵G是正三角形ABC的中心,且M为BC的中点,?
∴A、G、M三点共线,AM⊥BC.?
 ?
?
∵B1C1∥BC,∴B1C1⊥AM于G,即GM⊥B1C1,GA1⊥B1C1.?
∴∠A1GM是二面角A1-B1C1-M的平面角.?
∵点A1在平面BB1C1C上的射影为M,∴A1M⊥MG,∠A1MG=90°.?
在Rt△A1GM中,由A1G=AG=2GM,得∠A1GM=90°,即二面角A1-B1C1-M的大小是60°.?
(2)过B1作C1C的平行线交BC于P,则∠A1B1P等于异面直线A1B1与CC1所成的角.?
由PB1C1C是平行四边形得B1P=C1C=1=BP,PM=BM-BP=![]() ,A1B1=AB1=2.?
,A1B1=AB1=2.?
∵A1M⊥面BB1C1C于M,?
∴A1M⊥BC,∠A1MP=90°.?
在Rt△A1GM中,A1M=A1G•sin60°=![]() .?
.?
在Rt△A1MP中,A1P2=A1M2+PM2=(![]() )2+(
)2+(![]() )2=
)2=![]() .?
.?
在△A1B1P中,由余弦定理得?
cos∠A1B1P= .?
.?
∴异面直线A1B1与CC1所成的角为arccos![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
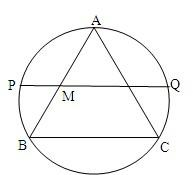 (选做题)(几何证明选讲)如图,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P、Q,则线段PM=
(选做题)(几何证明选讲)如图,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P、Q,则线段PM=
 如图,正△ABC的边长为15,
如图,正△ABC的边长为15, 如图,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AD和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
如图,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AD和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.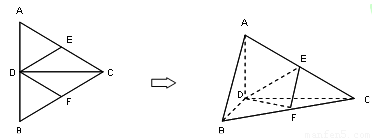
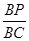 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.