题目内容
设函数h（x）=
其中f（x）=|x|，g（x）=-（x-1）2+3，则h（x+1）的最大值为（ ）
|
| A、0 | B、1 | C、2 | D、3 |
分析：本题考查的是的是分段函数问题．在解答时应先结合函数f（x）、g（x）的图象，根据所给分段函数的意义写出分段函数h（x）的解析式，进而求得函数h（x）的最大值，由于h（x+1）的图象可以看作由函数h（x）的图象向左平移1个单位得到．进而获得问题的解答．
解答：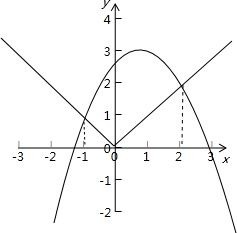
解：由题意可知：函数f（x）、g（x）的图象为：
由图象可知：函数h（x）的解析式为：
h(x)=
当x≤-1时，hmax（x）=-1；
当-1＜x≤2时，hmax（x）=2；
当x＞2时，h（x）＜2．
又由于h（x+1）的图象可以看作由函数h（x）的图象向左平移1个单位得到．
∴h（x+1）的最大值为2．
故选C．
解：由题意可知：函数f（x）、g（x）的图象为：由图象可知：函数h（x）的解析式为：
h(x)=
|
当x≤-1时，hmax（x）=-1；
当-1＜x≤2时，hmax（x）=2；
当x＞2时，h（x）＜2．
又由于h（x+1）的图象可以看作由函数h（x）的图象向左平移1个单位得到．
∴h（x+1）的最大值为2．
故选C．
点评：本题考查的是分段函数、二次函数、绝对值函数等知识的综合类问题．在解答的过程当中充分体现了分类讨论的思想、数形结合的思想以及问题转化的思想．值得同学们体会反思．
练习册系列答案
相关题目
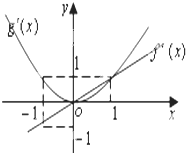已知函数f′（x），g′（x）分别是二次函数f（x）和三次函数g（x）的导函数，它们在同一坐标系下的图象如图所示，设函数h（x）=f（x）-g（x），则（ ）
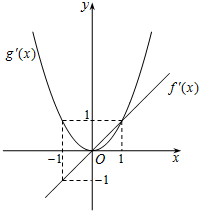（2013•武汉模拟）已知函数f'（x）、g'（x）分别是二次函数f（x）和三次函数g（x）的导函数，它们在同一坐标系下的图象如图所示：